單元大綱

    • 4-1．filtration

      The basic equation (Lewis equation) is

      　(4-1)

      v（m/s） filtrate flux，A（m2） Filtration area，V（m3） filtrate volume，t（s） filtrate time，μ（kg/m·s）Fluid viscosity，ΔP（Pa） Filtration pressure, Rm Filter material (filter paper or membrane) resistance coefficient，Rc （m-1）Resistance coefficient of filtration (cakes, solids deposited on filter media).

      The resistance coefficient of the filter media is constant if clogging does not occur during filtration operations. On the other hand, the cake resistance increases with the accumulation of solids on the filter media; if the cake is incompressible,

      Rc = αCV/A　 (4-2)

      α（m/kg）Cake resistivity，C（kg/m3） Concentration of solids in filtration stock solution

      From Equations 4-1 and 4-2, it follows that

      　(4-3)

      On an industrial scale, 'constant speed filtration', in which the pressure is controlled to maintain a constant flow rate of filtrate, and 'constant pressure filtration', in which the pressure is kept constant, are used.

    • 4-1-1．Constant speed filtration

      Since dV/dt = V/t in constant velocity filtration

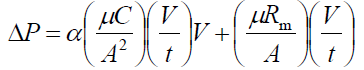      　(4-4)

      Therefore, the ΔP vs. V plot for constant speed filtration is a straight line, and the slope gives the cake resistivity α and the intercept gives the filter media resistance coefficient Rm.

      4-1-2．Constant pressure filtration

      Since ΔP is constant in constant pressure filtration

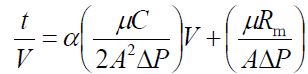      　(4-5)

      Equation 4-5 is called the Ruth equation. In constant pressure filtration, the plot of t/V vs. V is a straight line, and the slope gives the cake resistivity α and the intercept gives the filter media resistance coefficient Rm.

      4-1-3．gravity filtration

      Gravity filtration experiments often use "gravity filtration" with a filter paper and a funnel. In gravity filtration, the filtration pressure decreases in proportion to the filtrate volume, so

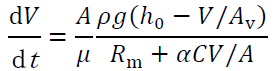      　(4-6)

      ρ（kg/m3）Fluid density，g （m/s2） acceleration of gravity，h0 （m） Liquid depth of filtration stock solution，Av（m2） Filter cross-sectional area

      Integrating Equations 4-6 from t = 0 to t and V = 0 to V

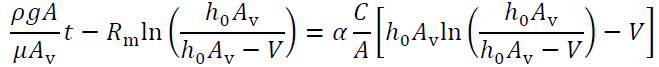      　(4-7)

      In Equation 4-7, the values other than α are equipment specifications, operating conditions, and experimental results, so a plot with the left side of the above equation on the y-axis and the values other than α on the right side on the x-axis is a straight line, and α can be obtained from the slope. Also, since C = 0 when the filtrate contains no solids,

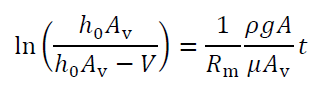      　(4-8)

      Therefore, applying Equation 3-8 to the results of the water transmission experiment, Rm is obtained from the slope.

    • 4-2．centrifuge

      The centrifugal force F acting on an object of mass m moving with angular velocity ω (rad) on a circumference of radius r is

      F = mrω² 　(4-9)

      When the centrifuge is operating at number of rotations N, the distance L travelled in one second by an object at r from the center is

      L = 2πrN 　(4-10)

      In many centrifuge specifications, the number of revolutions is expressed in r.p.m. (revolution per minute). In international units, it should be converted to r.p.s. (revolutions per second).Since an angular velocity of 1 rad is the angle formed by a solitary body of the same length as the radius

      ω = 2πrN/r = 2πN 　(4-11)

      From Equations 4-9 and 4-11, we see that

      F = 4mπ²N²r 　(4-12)

      The ratio of the centrifugal force to the universal gravitation force mg in Equation 4-12 is the centrifugal effect x.

      x = 4mπ²N²r /mg = 4π²N²r/g 　(4-13)

      Usually, centrifugal force is denoted as 10 G or 100 G, where the number denotes the centrifugal effect x and G denotes the gravitational acceleration. Gravitational acceleration is denoted by a capital "G" to distinguish it from mass (g).

      4π²N²r = xg ≡ xG　 (4-14)

      Since the driving force for a particle settling in a fluid in a centrifugal field is centrifugal force, the gravitational acceleration in the Stokes equation is replaced by Equation 4-14,

      　(4-15)

      Since the centrifugal force is a function of the distance r from the center of the axis of rotation to the particle

      ut = dr/dt　 (4-16)

      From Equations 4-15 and 4-16, one can determine the time it takes for the particles to settle to the bottom of the centrifuge tube by centrifugation.