Pourbaix diagram of sulfur (s)
單元大綱
-
-
E = 0.25 － 0.06648×pH (式1)
Equation 1 is shown in the graph below with pH on the horizontal axis and E(V) on the vertical axis. Note that the SO42-⇔HS- line (black thick line) in the figure is the boundary condition obtained above.
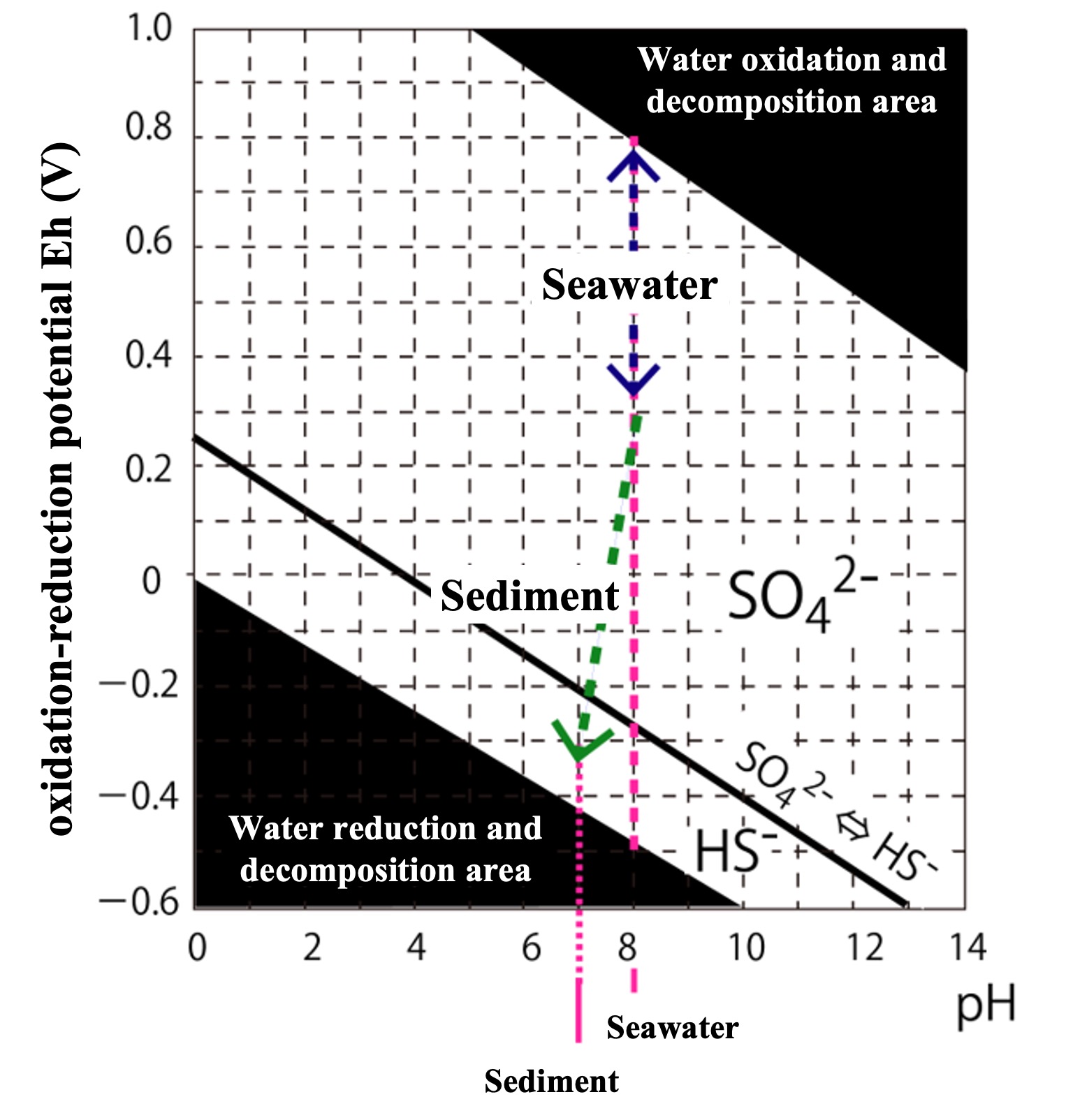
If we measure the oxidation-reduction potential of oxygen-rich seawater (pH 8), it is about +0.3 to +0.6 (V). (If only a sufficient amount of oxygen is dissolved in pure water, the oxidation-reduction potential of that water will be +0.8 (V), but since natural water also contains reducing substances (e.g., organic matter), it will be less than +0.6 (V) in sea water.)
From this figure, it can be determined that sulfur (S) is stable in oxygenated seawater (E = 0.3-0.6 V) as SO42-.
When oxygen is reduced to zero in the sediment, the redox potential suddenly drops to a low level. Furthermore, when oxidants such as nitric acid are also eliminated, the redox potential falls below the SO42-⇔HS- line. Sulfate-reducing bacteria, which breathe sulfuric acid (SO42-) as an oxidant, proliferate in the sediment, converting SO42- in the pore water to hydrogen sulfide (H2S). In the sediment, carbonic acid is produced as a result of organic matter decomposition, resulting in a slight acidification of the sediment to a pH of about 7. The redox potential and pH decrease in the sediment are indicated by the green dashed arrows in the figure. -
Earlier, we plotted the conditional equation [SO42-] / [HS-] = 1 (Eh = 0.25 - 0.06648 x pH) on a pourbaix diagram. What would happen with a different ratio.
Under the condition [SO42-] / [HS-] = 1000, Eh = 0.27 - 0.06648 x pH. The potential has shifted by +0.02. The figure is almost the same as the previous one. This means that the ratio of [SO42-] to [HS-] changes abruptly near this plot.
-
In addition, hydrogen sulfide ion (HS-) is in dissociative equilibrium with hydrogen sulfide (H2S).
Reaction equation for the dissociation equilibrium of hydrogen sulfide and hydrogen sulfide ion
H2S (aq) = H+ + HS- ；K = 10－7 （K is the dissociation equilibrium constant）
This is an acid-base reaction, since the oxidation number of S does not change in this reaction at -2 valence. Therefore, the redox potential is irrelevant in this dissociation equilibrium condition. The relationship between the equilibrium constant and pH is expressed by the following equation.
Equilibrium constant = {concentration product of the product form} / {concentration product of the original form} so,
[HS-][H+] / [H2S]} = 10－7
Take both sides Log and express the hydrogen ion concentration in terms of pH.
Log{ [HS-] / [H2S] } － pH = －7
The equilibrium condition where HS- and H2S coexist in the same ratio: [HS-] / [H2S] = 1 is at pH = 7.
Below pH 7, most will exist as H2S, and above pH 7, they will exist as HS-. I have rewritten the previous figure to add this information.
This is called the "Pourbaix diagram," which shows how the chemical form of a substance changes with pH and redox potential. The "water oxidative decomposition region" and the "water reduction decomposition region" are regions where H2O decomposes, and therefore cannot exist in an aqueous environment.
Again, the boundary conditions noted in the Pourbaix diagram are calculated from thermodynamic constants, and it has been confirmed that sulfate reduction can proceed even in more oxidizing environments (from about -0.1 (V)) due to microbial action. -
-