單元大綱

    • 4-1．ろ過

      基本式（Lewis 式）は，

      　(4-1)

      v（m/s） ろ液流束，A（m2） ろ過面積，V（m3） ろ液量，t（s） ろ過時間，μ（kg/m·s） 流体粘度，ΔP（Pa） ろ過圧力, Rm ろ材（ろ紙や膜）抵抗係数，Rc （m-1） ろさい（ケーク，ろ材上に堆積する固体）抵抗係数

      ろ材の抵抗係数は，ろ過操作中に目詰まりが起こらなければ一定である。一方，ケーク抵抗はろ材上への固形分の堆積とともに増加，ケークが非圧縮性の場合，

      Rc = αCV/A　 (4-2)

      α（m/kg） ケーク比抵抗，C（kg/m3） ろ過原液の固形分濃度

      式4-1 と式4-2 から，

      　(4-3)

      工業規模では，圧力を制御してろ液の流速を一定に保つ「定速ろ過」と，圧力を一定に保つ「定圧ろ過」が利用される。

    • 4-1-1．定速ろ過

      定速ろ過ではdV/dt = V/t なので，

      　(4-4)

      よって，定速ろ過のΔP vs V プロットは直線となり，傾きからケーク比抵抗α，切片からろ材抵抗係数Rm が得られる。

      4-1-2．定圧ろ過

      定圧ろ過ではΔP が一定なので，

      　(4-5)

      式4-5 はRuth 式とよばれ，定圧ろ過においてはt/V vs V のプロットが直線となり，傾きからケーク比抵抗α，切片からろ材の抵抗係数Rm が得られる。

      4-1-3．重力ろ過

      実験ではロートとろ紙を使った「重力ろ過」が多い。重力ろ過では，ろ過圧力がろ液量に比例して低下するので，

      　(4-6)

      ρ（kg/m3） 流体密度，g （m/s2） 重力加速度，h0 （m） ろ過原液の液深，Av（m2） ろ過器の断面積

      式4-6 をt = 0 からt，V = 0 からV で積分すると，

      　(4-7)

      式4-7において，α以外は，装置仕様，操作条件，実験結果なので，上式の左辺をy軸，右辺のα以外をx軸にとったプロットは直線となり，傾きからαが得られる。また，ろ過原液が固形分を含まない場合はC = 0なので，

      　(4-8)

      よって，水の透過実験の結果に式3-8を適用すると，傾きからRmが得られる。

    • 4-2．遠心分離

      半径r の円周上を角速度ω（rad）で運動する質量mの物体に働く遠心力Fは，

      F = mrω² 　(4-9)

      遠心分離機を回転数Nで運転しているとき，中心からrにある物体が1秒間に移動する距離Lは，

      L = 2πrN 　(4-10)

      遠心分離機の仕様書では回転数をr.p.m （revolution per minute）で表記していることが多い。国際単位では秒単位のr.p.sに換算すること。角速度1 radは半径と同長の孤がなす角度なので，

      ω = 2πrN/r = 2πN 　(4-11)

      式4-9と4-11より，

      F = 4mπ²N²r 　(4-12)

      式4-12の遠心力と万有引力mgの比が遠心効果xである。

      x = 4mπ²N²r /mg = 4π²N²r/g 　(4-13)

      通常，遠心力は10 Gや100 Gと表記され，数字が遠心効果xを，Gが重力加速度を表す。ここで，重力加速度を大文字のGで表すのは，質量のgと区別するためである。

      4π²N²r = xg ≡ xG　 (4-14)

      遠心場で流体中を沈降する粒子の推進力は遠心力なので，Stokes式の重力加速度を式4-14で置き換えると，

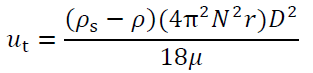      　(4-15)

      遠心力は，回転軸の中心から粒子までの距離rの関数なので，

      ut = dr/dt　 (4-16)

      式4-15と4-16から，遠心分離によって粒子が遠沈管の底に沈む時間を求めることができる。