1種の個体群動態

個体群動態の基本モデル
世代・時間
　冒頭のシミコの話から徐々に個体群動態の基本モデルへと解説していこう。シミコは最初の分裂で1個体から2個体となった。これは実は「1個体からもう1個体が分裂して増えた」のではなく、「１個体の体内で２個体が出芽して、その2個体が体外に出た結果、元の個体が死んだ」のである。クラゲの多くの種が、底生生活を送り無性生殖をおこなうポリプ期と、浮遊生活を送り有性生殖をおこなうメデューサ期をもつ (ただしシミコは例外的にメデューサ期に無性生殖をおこなう)。現実のクラゲの生活環は他にも色々と複雑だが、話を簡単にするために、シミコは分裂によって世代交代していると考えることにしよう。
　2個体に分裂した翌日に4個体になったのは、2世代目の2個体から各2個体が3世代目として分裂した結果である。ここで世代を時刻とよび、これをtで表す。そして時刻tにおける個体数をN_tとよぶことにする。では、この個体数の変化を数式で表現してみよう。
　t = 0における個体数N₀ = 1であり、それらが分裂して、t = 1で、N₁ = 2となった。元の個体が死んで個体数が減ったことも考慮しながら、これを数式で表すと以下のようになる。

N₁ = N₀ + (増えた個体数) – (減った個体数) = 1 + 2 – 1 = 2

t = 2のときの個体数も同様に考えられる。増えた個体数と減った個体数もN₁を使って表現すると、以下のようになる。

N₂ = N₁ + 2 x N₁ – 1 x N₁ = 2N₁

　ある時間に生まれた子が次の子を産むまでの一連のサイクル、生活環が個体群内の全個体で同調していて、世代が重複しない生物では、このように順に計算していけば、将来の個体数を予想できる。これを一般化して表現してみよう。時間tの世代と次の時間t + 1の世代の個体数変動は以下のように表せる。

N_{t + 1} = N_t + b N_t – d N_t 

ここでbは単位時間あたりの増加率、dは単位時間あたりの減少率である。この式の右辺をN_tでまとめると

N_{t + 1} = (1 + b – d) N_t

となる。さらに増加率と減少率の差b – dをまとめて純増加率Rとすると、 

N_{t + 1} = (1 + R) N_t        （6.1）

と表現できる。今度はN₂とN₀の関係を数式で表現してみると、以下のようになる。

N₂ = (1 + R) N₁ = (1+R) (1 + R) N₀ = (1 + R)² N₀

この式を一般化すると、時間tの世代の個体数は、時間0での個体数N₀とRで以下のように表現できる。

N_t = (1 + R)^t N₀        （6.2）

これが個体群動態の最も基本となるモデルである。じつは冒頭の計算は、

N₃₀ = 2³⁰ x 1

を計算したのだった。
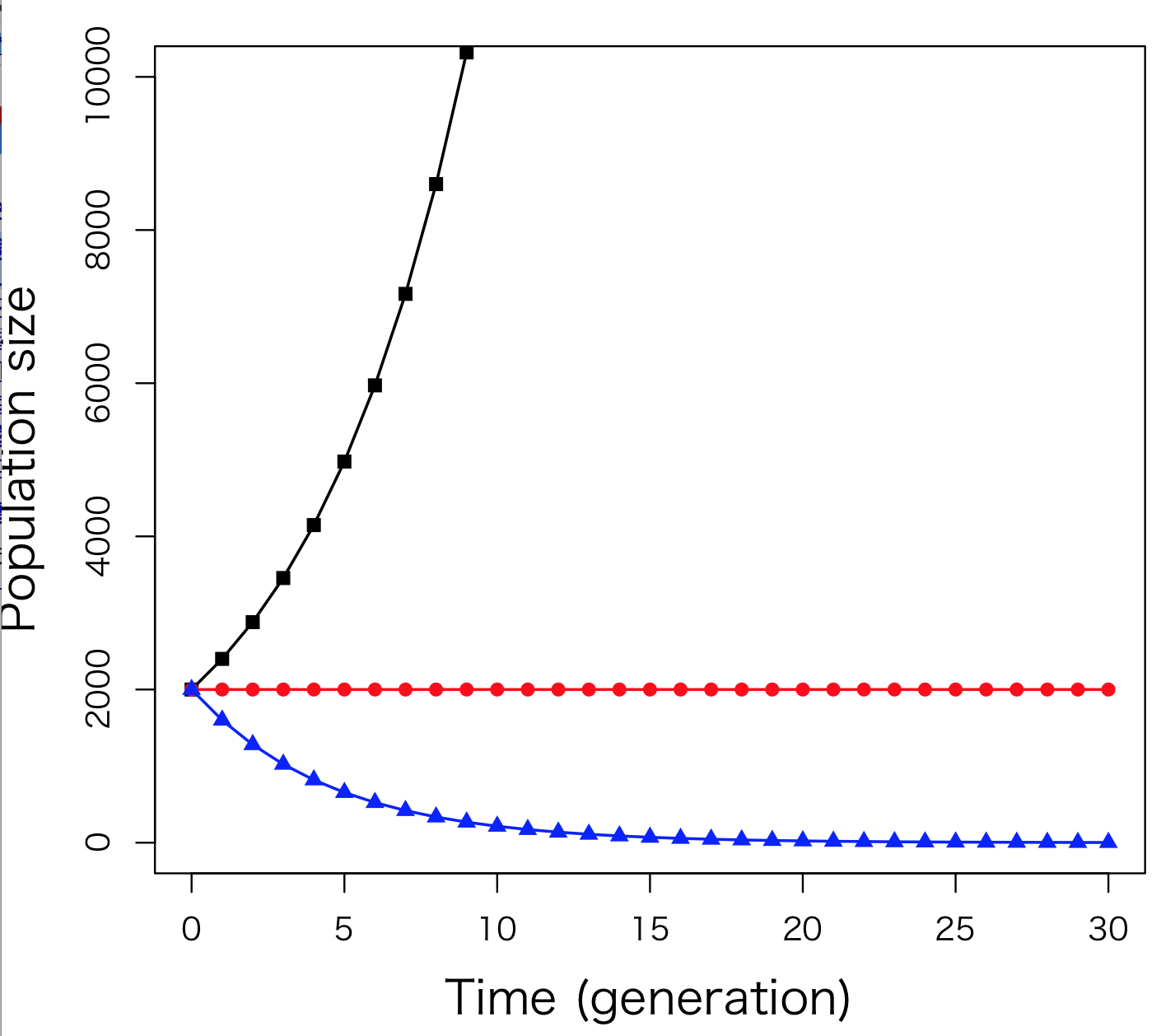
　6.2式はN_tとN₀の関係式、あるいはN_tとRの関係式だと考えることもできるが、ここでは個体数N_tと時間tの関係式だと考える。つまり、この式は個体群サイズの時間変動、つまり個体群動態を表した式なのである。N₀ = 2000として、N_tとtの関係を図示してみよう (右図)。Rが正の値をとるときは (黒の折れ線, R = 0.2)、個体数N_tが多くなるほど傾きが大きくなり、次の時間までに増殖する個体数が多くなる。一方、Rが負の値をとるときは個体数は減少し (青の折れ線, R = –0.2)、R = 0のときには個体群サイズは変動しない (赤の折れ線)。

内的自然増加率
　先ほどのシミコの話では「世代は重複しない」という筋書きにしていた。けれども、本当はシミコは昼でも夜でも分裂するので、世代が重複している。それぞれの親の繁殖のタイミングがずれているので、同時刻に大きい親個体もいればサイズの小さい個体もいる。そのため複数世代が同じ時刻に混ざっている。このように繁殖が同調せず世代が重複している場合の個体群動態を正確に予測するためには、時間の単位が短いほうがよい。時間の単位を極限まで短くしたとき、時間tにおける個体数の増殖率（dN/dt）は以下の微分方程式で表される。

\( \frac{dN}{dt} = rN \)           (6.3)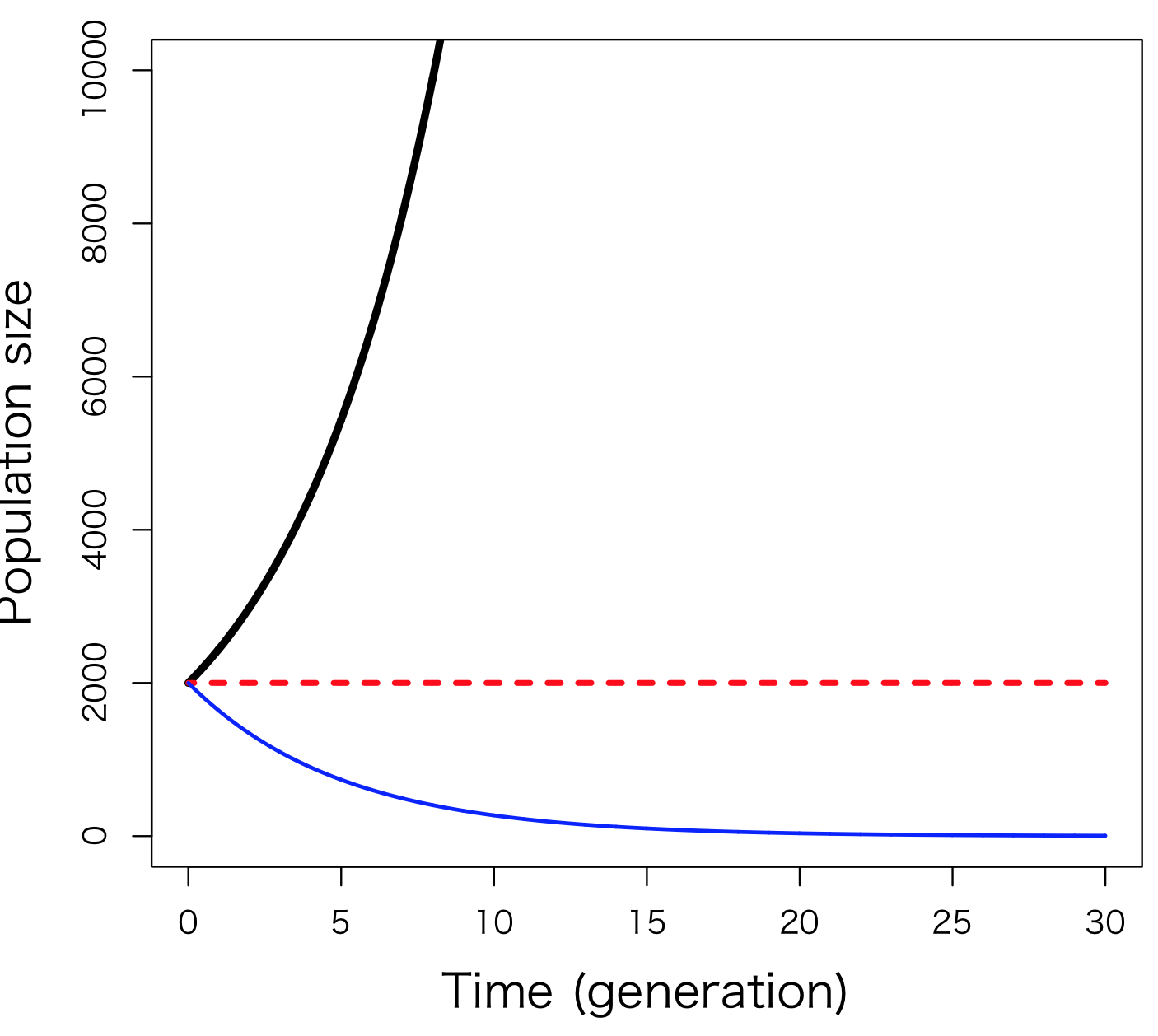

これは6.2式の微分方程式版である。dN/dtは、個体数が時間に応じて変化する様子を曲線として描いた場合の、ある時点における「傾き」である。また、この式で、rは6.1式に登場したRの微分方程式版であり、個体あたりの瞬間出生率から瞬間死亡率を引いた値である。rは内的自然増加率と名付けられている。6.3式で表される個体群動態も6.2式の個体群動態とよく似ていて (図6-2B)、r > 0であれば個体群は増加し、r < 0であれば減少する。r = 0のとき個体数は変動しない。
　ここまでの話では、r > 0でありさえすれば個体数は指数関数的に増える。つまり個体数の増加を抑えるような、現実の個体群動態で考えられる多くの要因が、まだ含まれていないのだ。次節からは、とくに種内関係と種間関係に注目しながら、個体数の増殖を抑える要因を挙げていこう。

密度効果・環境収容力
　生物が成長して子孫を残すためには、餌や生息場所、配偶相手などの資源を獲得しなければならない。しかし、資源は有限であり、質が大きく異なる資源もある。
　個体数が少ないうちは、資源の獲得は容易であり、良い資源を選ぶことができるので、個体群の成長率は高いだろう。
　一方、個体数が増えると個体群全体が資源不足になり、個体の成長速度や生存率、あるいは繁殖力 (産卵数) が低下して、個体群の成長率も低下していくことも予想される。個体群サイズがある個体数になると、成長率は0になり、個体数がさらに増えると成長率はマイナスとなるはずだ。これは、個体群を構成する個体の分布面積が、個体数に応じて大きく変化することがない、つまり個体数が増えるほど高密度となることも前提となっている。高密度になるほど成長率が低下する現象を密度効果という。
　ただし、個体群の増殖率は低密度ほど高いとはかぎらない。あまりにも密度が低いと、配偶相手が見つからず子孫を残せないこともあるからだ。また、集団で生息することによって乾燥などのストレスを緩和したり、捕食者に対する防衛効果が得られることもある。このような状況では密度が高くなるほど増殖率が上がる。この現象はアリー効果とよばれる。
　先ほどの微分方程式6.3式に改良して、密度効果を表現してみよう。まず、個体数が増えて増殖率が0になるときの個体数を定数Kとする。このときKを環境収容力という。餌や生息場所が豊富な場所ではKが大きく、乏しい場所ではKは小さい。個体数NがKになったときに、dN/dt = 0となる数式にすればよいのだから、6.3式に (K – N) という項を掛けてやればよさそうだ。けれども、rN (K – N) では困ったことになる。Nが小さいとき、(K – N) はKに近い値となるのだ。そうすると、Nが小さいとき、rN (K – N) の値はrNに比べてとても大きな値になってしまう。そこで、(K – N) をKで割った項を6.3式に掛けたのが以下の式である。

\( \frac{dN}{dt} = rN \frac{K - N}{K} \)        (6.4)

　6.4式のモデルでは、個体数が少ないうちは (K – N)/Kが1に近い値をとるため、6.3式に近い増殖率を示す。しかしNが大きくなると(K – N)/Kが0に近づくため増殖率dN/dtが低下し、N = Kとなったところで増殖率が0になる。そのため、最初の個体数が少ないとき、個体群動態は図6.2Dの黒の曲線のようなS字型となる。このようなS字型の曲線をロジスティック曲線という。もちろん、最初の個体数が多ければS字の下が途切れたような曲線となるし、最初の個体数がKを超えていた場合は、(K – N)/Kが負になるため個体群サイズは減少して、N = Kとなったところで増殖率が0になる。
　また、dN/dtをY軸、個体数NをX軸として6.4式を図示すると負の二次関数となっていることにも注目しよう。Nが0あるいはKのときdN/dt = 0となり、0.5KのときdN/dtは最大値となる。Nが0より大きくK未満の範囲では、dN/dtがプラスであるため、個体数が増加する。一方、NがKを超えるとdN/dtがマイナスになり個体数は減少する。個体数が0でなければ、この個体群の個体数は最終的にKで安定となる。このように、微分方程式を図示してみると、個体群が増える条件や減る条件、そして一定数で安定する条件を知ることができる。
　6.4式は多くの複雑な個体群動態モデルの基礎となるモデルである。しかし、現実の個体群動態を表現するためには、6.4式はまだまだ単純すぎる。じつは6.4式は、(1) 環境条件や資源に変動がないこと、(2) 個体群を構成する個体の形質に変異がないこと、(3) 個体の移出入や進化が起こらないこと、(4) 密度効果が個体数変動にタイムラグなく応じて作用すること、(5) 種間関係もないことなどを暗に前提としている。実際は、温度などの環境条件が変動し、餌となる生物の個体数も変動する。さらに、例えば高密度による餌不足が成長速度や産卵数の変化となって現れるのは、高密度となってから少し時間が経った後だろう。つまり密度効果にはタイムラグがある。種間競争や捕食・被食関係を想定したモデルは、6-2節で紹介しよう。
　6.4式とは少し違う状況を想定した単純なモデルとして、最初に紹介した世代が重複しない個体群動態のモデル (6.1式) に密度効果を組み込んでみよう。まず、6.1式を以下のように書き換える。

N_{t + 1} = N_t + N_t R        （6.1）

ここで、個体群の純増加率Rに、6.4式同様の密度効果 (K – N)/Kを掛けると、以下の式になる。

\( N_{t + 1} = N_t + N_tR \frac{K - N_t}{K} \)        (6.5)

興味深いことに、6.5式の個体群動態は一筋縄ではいかない。6.4式と同じように、個体数が環境収容力Kに収束していく結果になることもあるが (図6-2C)、これは、Rが小さい場合にしか起こらないのだ。Rが大きい場合には、個体数が増加しすぎてKを超え、次の時間では個体数が減少しすぎてKを下回るなどという事態が生じる (図6-4)。Rに色々な値を入れてみると、個体数が減衰振動しながらKに収束する場合 (図6-4A) や2つの個体数を交互に繰り返す2点周期 (図6-4B)、4点周期 (図6-4C)、そして初期値の小さな違いによって個体群動態が大きく変化するカオス (図6-4D) へと、個体群動態のパターンがRに応じて変化していくことが分かる。言い換えると、非生物的な環境条件が完全に安定していて、他種の影響が全くなかったとしても、ただ密度効果があり増殖率が高いだけで、個体群動態は不安定になり、絶滅する場合さえある (図6-4Dのシミュレーションでは絶滅が起こっている)。