Calculation of "possible dissolved DIC concentration" before and after the formation of calcium carbonate particles
①Calculate the concentration of DIC that can be dissolved in seawater before calcium carbonate is formed
②Calculate the concentration of DIC that can be dissolved when calcium carbonate forms and alkalinity changes
Calculate the DIC concentration that will be surplus from the difference between ① and ②.
① DIC concentration that can be dissolved before calcium carbonate is formed in seawater
Find the total carbonic acid concentration 【DIC】 that can be dissolved in seawater when the alkalinity of the seawater before calcium carbonate (CaCO3) is formed is 2.3 mmol/L.
There are enough weak electrolyte ion charges in seawater to balance alkalinity. For simplicity, the weak electrolyte ions that balance alkalinity are CO32- and HCO3-.
Alkalinity = 2【CO32-】+【HCO3-】= 2.3 mmol/L
The 【DIC】 we want to find now is also mostly CO32- and HCO3-, so for simplicity, we do the following.
【DIC】 = 【CO32-】+【HCO3-】
In the previous problem (percentage of dissolved carbonic acid components in seawater), we determined that at pH 8 of seawater, about 10% of the total carbonic acid is present as CO32- and about 90% as HCO3-. So, if we let 【DIC】 = 10C,
【CO32-】=C,
【HCO3-】=9C.
From the above,
Alkalinity: 2.3 mmol/L = 2【CO32-】+【HCO3-】
= 2C + 9C = 11C
C = 0.209 mmol/L、 【DIC】 = C + 9C = 2.09 mmol/LThis is the value of the DIC concentration (2.09 mmol/L) dissolved in seawater pH 8 with an alkalinity of 2.3 mmol/L.
The same calculation procedure and results are summarized in the column below.

② concentration that can be dissolved in seawater when calcium carbonate (CaCO3) is formed
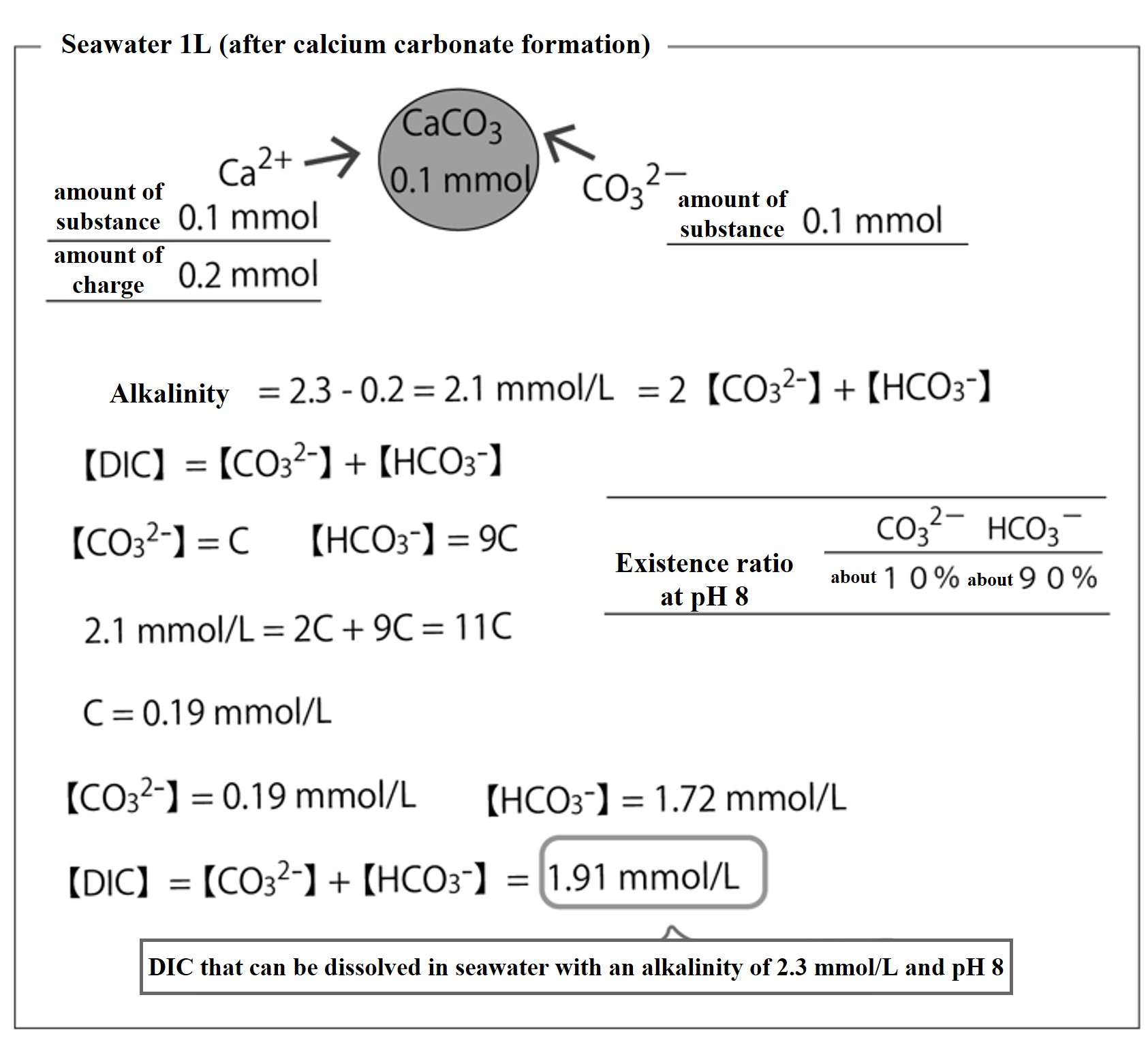
Calculate the DIC concentration that can be dissolved in seawater when 0.1 mmol of calcium carbonate (CaCO3) is formed in 1L of seawater with pH 8 and alkalinity of 2.3 mmol/L.
Since calcium is a divalent cation, if 0.1 mmol of CaCO3 is formed in 1 L of seawater, the alkalinity of the seawater is reduced by 0.2 mmol/L. Thus, the alkalinity becomes 2.3 - 0.2 = 2.1 mmol/L,
Alkalinity 2.1 mmol/L = 2【CO32-】+【HCO3-】.
If the pH8 of seawater does not change, then 【CO32-】=C and 【HCO3-】=9C, as in case ①,
from 2.1 mmol/L = 2【CO32-】+【HCO3-】= 2C + 9C = 11C,
C = 0.191 mmol/L 【DIC】 = 1.91 mmol/L.This means that if the seawater pH remains at pH 8 and the alkalinity becomes 2.1 mmol/L, the DIC concentration that can be dissolved in that seawater is 1.91 mmol/L.
The same calculation procedure and results are summarized in the column below.
To summarize the above,
The DIC that can be dissolved in the original seawater (pH 8, alkalinity 2.3 mmol/L) is 2.09 mmol/L. If 0.01 mmol of CaCO3 is formed in 1L of this seawater, the alkalinity is reduced to 2.1 mmol/L. At this time, the possible dissolved DIC is reduced to 1.91 mmol/L.
The formation of calcium carbonate reduces the possible dissolved DIC by 0.18 mmol/L. This means that the amount of DIC must be removed from the seawater. Since 0.1 mmol/L of DIC has already been removed when the CaCO3 shell is formed, another 0.08 mmol/L must be removed. If this seawater is in contact with the atmosphere, the excess (0.08 mmol/L) is released into the atmosphere.
The same calculation procedure and results are summarized in the column below.

More precisely,
Changes in the pH of seawater and the presence of boric acid must also be considered. The calculations assume that the formation and dissolution of calcium carbonate particles in 1 L of seawater does not change the partial pressure of carbon dioxide in the atmosphere. In the example above, we assumed pCO2 = 452 μatm constant. Near future. If the same amount of calcium carbonate particles is formed as above, the pH of that 1L of water will change from 8.00 to 7.97. The DIC that will be surplus before and after the formation of calcium carbonate particles is calculated to be 0.174 mmol/L, taking into account the presence of boric acid and the change in pH. That is almost the same as the 0.18 mmol/L resulting from the simple calculation above. (Details of the calculation are given in the "Development section".)

