High-energy cosmic rays are emitted from supernova explosions and other events in the universe. When these cosmic rays hit air molecules in the upper atmosphere, the atomic nucleus is broken and neutrons are ejected. When the neutron strikes a nitrogen atom and is replaced by a proton in the nucleus, it becomes 14C. The neutrons in radioactive 14C eventually β-decay (eject electrons) to protons, which return to 14N.

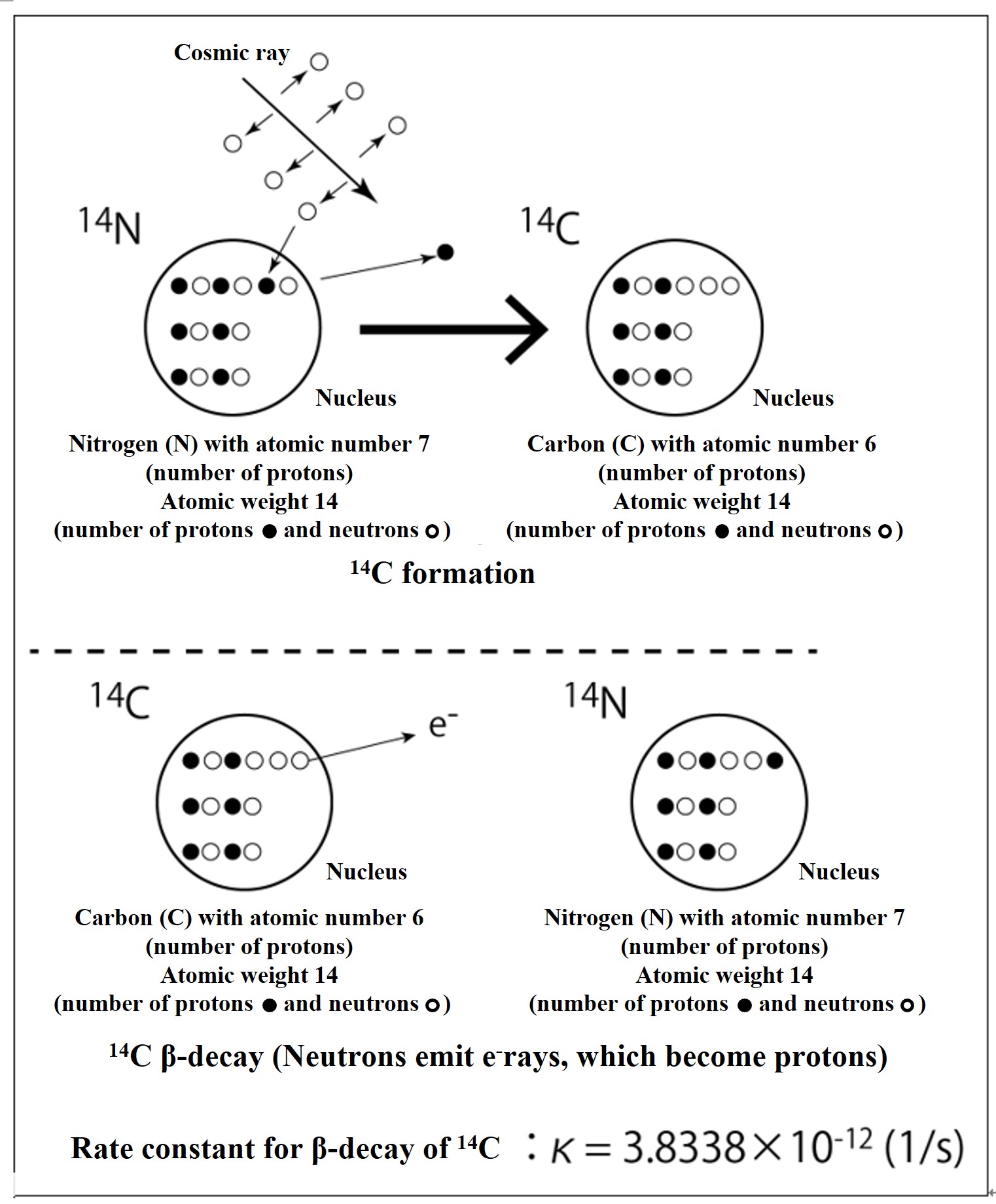
Figure 2

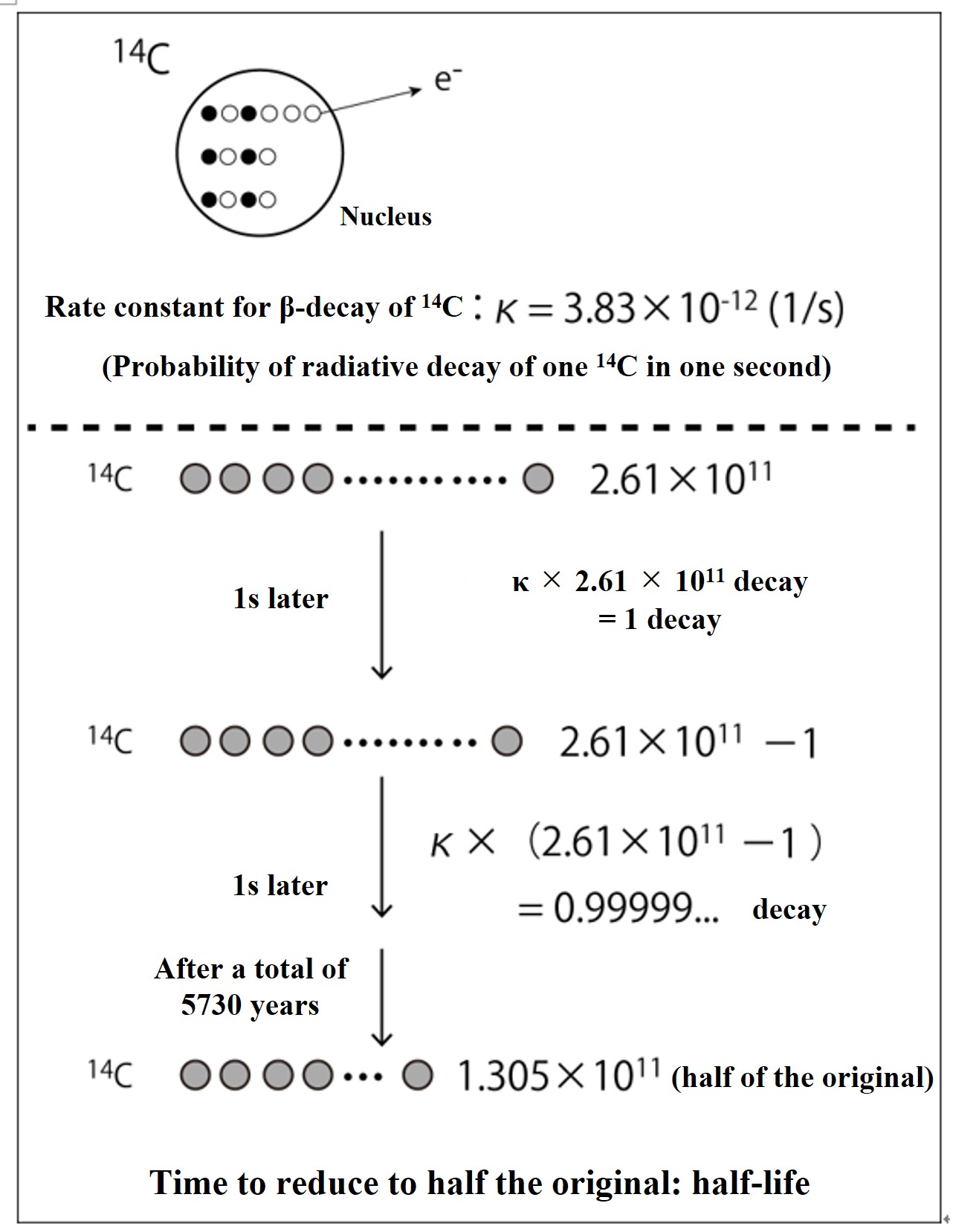
The probability of β-decay of 14C is the same everywhere in the universe forever, and the probability of radiative decay of one 14C atom in a unit of time (1 second) is shown in the above figure as the rate constant of β-decay, κ (= 3.83×10-12 (1/s)). If there are 2.61 x 1011 14C atoms, then after 1 second, only κ x 2.61 x 1011 atoms will β-decay and disappear (that amount of 14N atoms will be formed). To calculate this, out of 2.61 x 1011 14C atoms, exactly one 14C atom will disappear by radioactive decay after 1 second (that amount of 14N will be formed). The time it takes for the number of 14C atoms to be reduced to half of the original number is called the "half-life" due to radioactive decay. For 14C, that is 5730 years.

Figure 3

This will be converted to a mathematical equation. As you are learning the basics of marine chemistry, you will also forget the basics of calculus, so let's review them below.

　Let [14C]t denote the number of 14C atoms at a given time t. Then, the number of 14C atoms that disappear by β-decay in 1 second is κ × [14C]t. The number of atoms [14C]t+1 after 1 second is the initial number of atoms [14C]t minus the number of atoms that disappear κ × [14C]t. The formula is [14C]t+1 = [14C]t - κ × [14C]t.

　Transforming this, we get [14C]t+1 - [14C]t = -κ × [14C]t. The left side is the change in the number of pieces after 1 second. If we consider the denominator 1 (s) on the left side, it means that the change in number per second ([14C]t+1 - [14C]t)/1(s) is equal to -κ × [14C]t. That is, ([14C]t+1-[14C]t)/1(s) = -κ × [14C]t.

　Next, if the number of pieces changes not per 1(s) but per differential time ⊿(s), we get [14C]t+1-[14C]t)/Δ(s) = -κ × [14C]t.

　If the differential time ⊿ is infinitesimal, it can be expressed in the differential form d[14C]t / dt = -κ × [14C]t. The solution of this differential equation is the result shown in the figure below. (Please review the solution formulas for this differential equation on your own so that you can write them down smoothly.)

Figure 4

　Since the half-life is the time T that is half (0.5[14C]0) of the number [14C]0 at the initial time (t = 0), the half-life of 14C is calculated to be 5730 years, as shown in the figure below.

Note　In 14C dating, the half-life of 14C is calculated as 5568 years; there is an agreement to use the half-life (5,568 years) used by W.F. Libby (Nobel Prize winner in 1960), who discovered that 14C occurs naturally.

Figure 5

最終更新日時: 2023年 07月 20日(木曜日) 09:14