單元大綱

  • 展延 展延

    一般

    全部收合 展開全部
  • 展延 展延

    誤差の伝搬（正式版）

    • 　先のコース（有効数字を含む計算～簡易版～）では、有効数字より下の桁に含まれる誤差(±0.5や±0.05)が演算により、どれだけ伝搬するかを簡易的に求めたものです。分析化学の容量器具によっては、容量誤差が±0.1とか、±0.02とかマチマチです。累乗や対数計算を含む場合、どのようにしたらよいのでしょうか？


      　演算で伝搬される誤差を、より正確に計算するには、以下の公式を使います。

      誤差σ1～σn 含む数値（ x1～ xn ）の演算により伝搬される誤差（σ）：


       σ =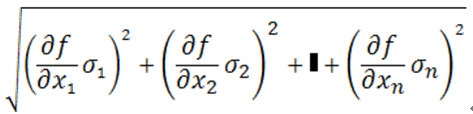 


      ルートの中の■は、x3以下も同様に、(    )2 が入ることを意味します。




    • なんだか、よくわかりませんよね。

      具体例をみれば、わかります。


      例題１）　二つの数値の足し算での誤差（σ）の伝搬を正式ルールで求めてください。


      数値x1は±σ1の誤差を持ちます。

      数値x2は±σ2の誤差を持ちます。

      数値x1とx2を足したときの誤差はどのようになるでしょうか？


      つまり、以下の式を計算したときの数値（x1 + x2）が持つ誤差「±σ」を求めたいのです。

      (x1 ± σ1) + (x2 ± σ2) = (x1 + x2 )± σ


      f = x1 + x2 として、

      正式ルール：σ = 　　に代入します。n=1とn=2 のところだけ使います。


      σ = ±  =  ± 


      引き算でも同じです。




    • 例題２）　誤差をもつ数値x1とx2の引き算してください





      例題３）誤差をもつ二つの数値x1とx2をかけてください



      （ルートの中は、各自計算して確認して下しさい）



      誤差をもつ二つの数値x1とx2について、それぞれの数値の最大値（x1 + σ1、x2 + σ2）と最小値（x1 - σ1、x2 - σ2）を求めます。

      最小値同士をかければ計算結果は最小になります。最大値同士をかければ計算結果は最大になります。その最小と最大が誤差を含めた計算結果になります。

      　




    • 例題４）　誤差を含む数値の割り算をしてください