有効数字（簡易ルールの応用問題）

Section outline

• Select section সাধারণ

  Collapse Expand

  সাধারণ

  সব গুটিয়ে ফেলুন সকল প্রসারণ করুন

  • Select activity English

    

    English URL
• Select section 有効数字を考慮した計算の応用問題

  Collapse Expand

  有効数字を考慮した計算の応用問題

  • Select activity 応用問題：　以下の測定により、海水中の粒子に含まれる炭素成分の含量(%：炭素量(g)/粒子乾燥重量(...

    
    

    応用問題：

    　以下の測定により、海水中の粒子に含まれる炭素成分の含量(%：炭素量(g)/粒子乾燥重量(g))と海水中濃度(mol(C)/L)を有効数字を考慮して計算しなさい。

     

    　海水1.00L (有効数字の桁数3桁)をメスフラスコで量り採り、その水をガラス繊維フィルターでろ過して、ろ紙上に残った物（残渣物）の乾重量を測定しました。つづいて、酸素雰囲気内で白金触媒により高温でフィルターを燃焼して、炭素成分を全て二酸化炭素にしました。その二酸化炭素濃度を測定して、フィルター上の粒子状物質に含まれる炭素量に換算します。

    
    

    
    

     

    
    

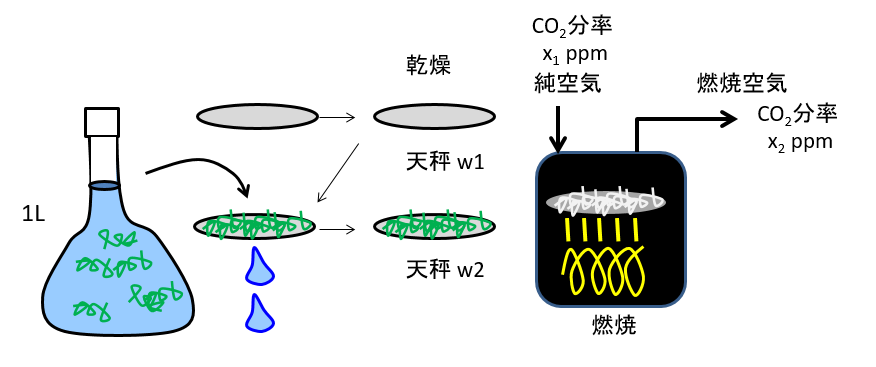
    ガラス繊維フィルターの乾燥重量（使用前）              ：w₁ = 1.0014 g

    海水をろ過して乾燥させた後のフィルター乾燥重量   ：w₂ = 1.0021 g

                                       (w₁とw₂の有効数字の桁数は6桁)

     

    フィルターを高温で燃焼してCO₂を発生させ、燃焼空気中のCO₂濃度を測定

     

    燃焼空気中（燃焼前）のCO₂モル分率  ：x₁ = 1 ppm

                                              (有効数字の桁数1桁)

    燃焼空気中（燃焼後）のCO₂モル分率  ：x₂ = 21040 ppm

                                              (有効数字の桁数5桁)

    燃焼空気のモル数　                 ：y = 0.013 mol

                                              (有効数字の桁数2桁)

     

    （補足．燃焼セルに送る空気(燃焼空気)のモル数はマスフローコントローラーで調節可能）

     

    計算式

    フィルター上粒子の乾燥重量(g)      ：A = w₂ – w₁

    燃焼空気中のCO₂モル分率の差分      ：B = x₂ – x₁  (ppm)

    燃焼したCO₂のモル数                ：C = y×(x₂ – x₁)×10^-6

    燃焼したCO₂の重量(g)               ：D = y×(x₂ – x₁)×10^-6/FW_CO2,

                                FW_CO2はCO₂の式量(44.01)で定数とする

    乾燥粒子に含まれる炭素含量(%)      ：E = D/A×10² (%)

    海水中粒子の炭素濃度(mol(C)/L)     ：F = C/1.00
    

     
    

    EとFを有効数字に注意して計算する。

     

    A = 1.0021 – 1.0014

    B = 21040 – 1

    C = 0.013×B×10^-6

    D = 0.013×B×10^-6/44.01

    E = 0.013×B×10^-6/44.01/A ×10² (%)

    F = 0.013×B×10^-6/1.00

     

    まず、加減算を計算する

           A = 1.0021 – 1.0014         = 0.0007 (g)

                                       (有効数字の桁数1桁)

           B = 210400 – 1              = 21039  (ppm)

                                       (有効数字の桁数5桁)

    （AとBに使われる値の有効桁の最小の位は、小数点4位と1の位で、其々一致している。そのまま計算すればよい）

     

             E = 0.013×21039×10^-6/44.01/0.0007×10²  = (0.887807965....)

    有効数字桁数：2桁,   5桁,             1桁

                         ※定数44.01については、有効数字を考慮しない

    有効数字の桁数の最も小さなもの：1桁

    （有効数字の最下位より、一桁低いところの数値0.88780..の8を四捨五入

     

    乾燥粒子に含まれる炭素含量(E)：0.9 (%)　（有効数字の桁数1桁）

     

             F = 0.013×21039×10^-6/1.00 = (273.057×10^-6) = 0.000273057)

    有効数字桁数：2桁,   5桁,      3桁

    有効数字の桁数の最も小さなもの2桁

     

    海水中粒子の炭素濃度(F)：2.7×10^-4 (mol(C)/L)　（有効数字の桁数2桁）

                         (もしくは、0.27 (mmol(C)/L)

    
    

    /////////////////////////////////////////////////////////////////

  • Select activity この応用問題のまとめ   与えられた数値 フィルター乾燥重量（使用前）：...

    この応用問題のまとめ

     

    与えられた数値

    フィルター乾燥重量（使用前）：w₁ = 1.0014 g        （有効数字の桁数5桁)

    フィルター乾燥重量（使用後）：w₂ = 1.0021 g        （有効数字の桁数5桁)

    CO₂モル分率（燃焼前）       ：x₁ = 1 ppm         (有効数字の桁数1桁)

    CO₂モル分率（燃焼後）       ：x₂ = 21040 ppm     (有効数字の桁数5桁)

    燃焼空気のモル数　          ：y = 0.013 mol      (有効数字の桁数2桁)

     

    途中計算

    A = 1.0021 – 1.0014  = 0.0007 (g)                (有効数字の桁数1桁)

    B = 210400 – 1       = 21039  (ppm)              (有効数字の桁数5桁)

     

    計算結果

    炭素含量(E)：0.9 (%)                             （有効数字の桁数1桁）

    炭素濃度(F)：2.7×10^-4 (mol(C)/L)                 （有効数字の桁数2桁）

     

    　炭素含量(E)の有効数字の桁数が1桁になったのは、途中計算Aの有効数字(1桁)に由来します。電子天秤では、6桁の精度で重量を測定したのに、その差分が１桁でしか得られなかったからです。

     

    　炭素濃度(F)の有効数字の桁数が2桁になったのは、与えられた数値で、燃焼空気のモル数の有効数字(2桁)に由来します。

     

    　このように、分析結果の数値の誤差要因を追跡すれば、分析操作の何処を改善すれば精度向上につながるのか判明します。この例では、より高精度の電子天秤を使うこと、燃焼空気のモル数（マスフローコントローラー）の精度を上げることが精度向上につながることが分かりました。