章节大纲

  • 折叠 展开

    常规

    全部折叠 展开全部

    授業資料（教科書PDF）は、こちらよりダウンロード

  • 折叠 展开

    検出限界と定量下限の決め方

    • 実は、ある分析法で、検出限界や定量下限については、ある決ったやり方があるわけではない。

      しかし、いくつか指針みたいのはある。このような曖昧な状況なので、環境分析化学のどの教科書にも検出限界と定量下限の決め方の説明がないのである。（あったとしても、強度法（検量線法）の原理を説明するだけ）　そこで、私なりに、以下に指針をまとめた。


      　下の絵のように、ブランク試料を測定したとき、
      ①　ピークらしきものが検出されない場合
      ②　小さなピークが検出される場合
      これら二通りについてイオンクロマトグラムを例として示す（下絵）。






    • ①ブランク試料を分析したとき、ピークらしきものが検出されない場合


      　イオンクロマトグラフィーで水溶性イオン成分を計測したときのクロマトグラムです。何かしらイオン成分分離されていれば、どこかの時刻（横軸）で電気伝導度（縦軸）にピークが表れます。下の図は、ブランク試料（イオン成分を含まない水）のクロマトグラムなので、イオン成分のピークが見られません。

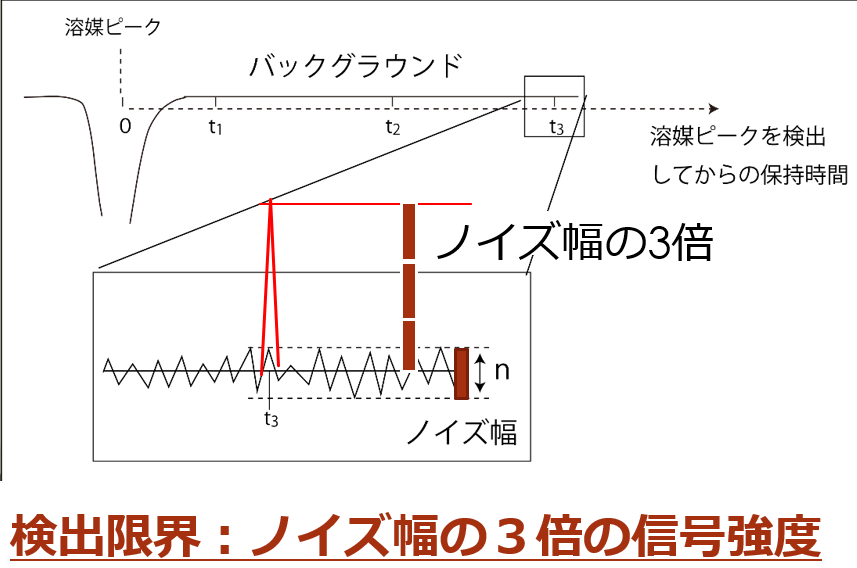
      　しかし、クロマトグラムのベースラインを拡大してみると、電気伝導度の計測では、バックグランドのノイズが発生していることがわかります。




      　このように、ブランク計測において、何ら、ピークが表れないケースにおいて、何か環境試料を計測したとします。その試料中に、ごく微量なイオン成分が含まれているとすれば、小さなピークが見られるはずです。そのとき、その小さなピークが、バックグラウンドのノイズ（noise）に対して、有意に大きなピーク（シグナル：signal）であるか？　を判定するため、signal / noise 比（S/N比）を使って検出限界の条件を定めます。


      検出限界：

      　S/N比=3を検出限界と定めます。平均ノイズ幅nを求めて、3nに相当するピーク(s)を検出限界とします。それよりも大きなピークをシグナルと認め（検出）、それよりも小さなピークはノイズなのか、シグナルなのか判定できない（不検出）。





      定量下限 ：

      　検出限界の条件をクリアしていることが前提になります。そのうえで、標準試料測定により検量線をつくり、その検量線上にプロットされる範囲が定量可能と判定されます。ただし、標準試料測定の繰り返し測定により、信頼性（精度）が担保されていることも必要です。例えば、定量可能範囲を、「検出限界を満たしていて、標準試料の繰り返し測定による誤差（変動係数）が 5 % 未満であること」　と定めることがあります。その定量可能範囲の下限を、定量下限といいます。



      超低濃度の標準試料が作れない場合の例外的な措置

      　ただし、環境分析においては、環境試料中の対象成分の濃度があまりに小さすぎるため、そのような低濃度の標準試料を作るのが不可能な場合もあります。例えば、大気中の不安定化合物（ジヨードメタンなど）の標準となる気体試料を作ることができません。そのような場合は、S/N比=10を定量下限と定めることもあります。平均ノイズ幅nを求めて、10nのシグナル(s)を定量下限とします。

      ※　ガスクロマトグラフ質量分析では、経験的に、S/N比が10以上であれば、検量線が直線性になり、かつ再現性が認められることが多いからです。そこで、S/N=10を定量下限とすることがあります。



    • ②　ブランク測定で原因不明ながらピークを示す信号強度があるとき


      　ブランク試料（対象成分が含まれない試料）を測定しても、何らかの原因でピークが検出される場合があります。試料処理や分析ラインからの対象成分が汚染することが原因のことが多いです。このような場合は、ブランク測定を10回繰り返し、ブランクの信号強度の標準偏差σを求めます。




      　ブランク測定で現れるピークの信号強度が何回計測しても全く同じなら、未知試料計測でも、その分、信号強度がプラスされている（下駄を履いている）と考えられます。そうであれば、未知試料の測定結果から、そのブランクの信号強度を差し引けばよいのです。ただし、ブランクを繰り返し測定して、その繰り返し再現性を確認する必要があります。とくに、ブランクに対して、有意な差を持つのか（検出しているのか）を確かめる必要があります。


      　ブランク測定を複数回測定した結果の例を下の図で示します。ブランク測定でみられるピークの大きさにバラつきがあることがわかりました。下の図では、ブランクの繰り返し測定による平均値を ” ave ”、標準偏差を " σ " で表しています。　




      　ブランク測定によるばらつきを考慮して、「ブランク測定の平均、プラス、標準偏差の３倍」のピークであれば、ブランクのピークに対して有意な差があると認められるだろう。ということで、下の図のように、検出限界値を、ave + 3σ　と定めます。（分析の目的により、ave + 10σ　などと定めることもあります）

      　　



      もちろん、ブランク測定でピークがみられるときでも、定量可能範囲については、

      「検出限界をクリアしたうえで、信頼できる検量線上にプロットされる範囲」

      定量下限は、定量可能範囲の下限、となります。