Rangkaan topik

  • General

    Tutup semua Kembangkan semua

  • 検出限界（下限）と定量下限

    • 検出限界と定量下限

      　この二つの言葉は、厳密に使い分けて、内容を理解しなければなりません。将来分析化学に携わらないにしても、理系人ならば知らなくてはならない大事なことを含んでいます。

       

      　2011年の原発事故の際、報道機関が「〇×から放射性物質が検出されました！」と一斉に報道して世間を騒がせました。ここで、あえて“騒がせた”と記したのは、報道機関のリポーターたちが“検出”という科学用語を理解しているとは到底思えない報道っぷりだったからです。検出限界値とその定義を示したうえで“検出されました！”と報道したところがあったでしょうか。せめてテレビ画面の端っこでもいいので、検出限界値を記すべきです。皆さんは理系人として生きてゆくのだから、“検出”の概念は理解してください。

       

      ※　放射性物質の検出に用いられる放射線計測には、“ゆらぎ”や“バックグラウンド”が存在します。放射線科学に基づき、“検出”を厳密に定義しなくてはなりません。私はその辺は詳しくないので、放射性物質の検出の説明はスルーさせてもらいます。もっと一般的な分析化学における検出とか定量についての説明を続けます。

       

      検出限界：

      　ブランク試料を測定したときの信号強度に対して、未知試料や標準試料を測定したときの信号強度が大きく、有意に区別できる限界のことです。

       

      定量下限：

      　未知試料や標準試料を測定したとき対象成分の信号強度を有意に検出したうえで、濃度を求めるのに足りるだけの信頼性を有する下限のことです。


      定量上限：

      　濃度を求めるのに足りるだけの信頼性を有する上限のことです。

       

      定量範囲（定量下限から上限までの範囲）：

      　定量下限から上限までの範囲のことです。検量線に直線性があることが理想的です。また、同一試料を繰り返し測定して、ある程度の再現性（精度）が保証される必要もあります。ただし、検量線を二次曲線や指数関数で求めることもありますが、この場合は変動が大きくなることもあるので注意が必要です。


      測定の目的に応じて、各分析者が検出限界や定量範囲を定めます。

      その科学的な根拠や限界値を報告書にシッカリ記すことが大事です。



  • Topic 2

    • 例題１－１）のプロットを再び示します。


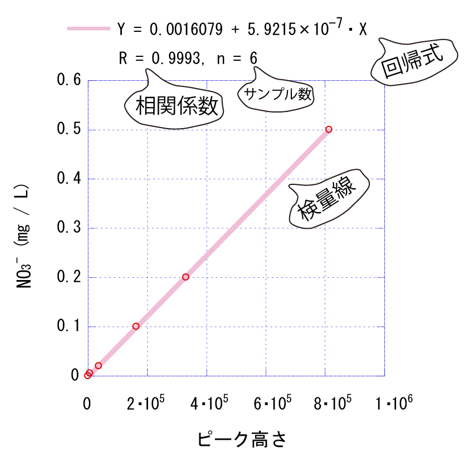
      原点に近い低濃度のところも、検量線上に乗っているようにもみえます。

      低濃度範囲を拡大してみましょう。



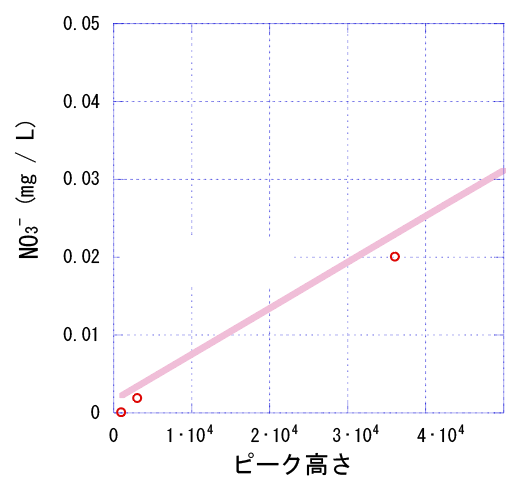
      　拡大前は、全てのプロットが検量線上に乗っていたように見えました。しかし、低濃度範囲を拡大してみると、低濃度のプロットでは検量線から少しずれていることが判明しました。

      　このような場合、低濃度の未知試料の信号強度（ピーク高）を、先の検量線の回帰式に代入して濃度を求めると誤差が大きくなってしまいます。このプロットが検量線上に乗らない理由を考える必要があります。

      ① 偶然な誤差に起因するのか

      ② 偶然ではなく何度測定しても同じように検量線からずれるのか


      二通りにわけて考えてみましょう。


      まず、②から対処してみます。

      　②の問題を解決する方法の一つとして、低濃度範囲をもカバーした検量線をつくることです。一直線の検量線の上には乗らないにしても、その測定に信頼性が確認されれば、そのような方法をとることができるでしょう。例えば、低濃度範囲の標準試料だけで作成した検量線と、高濃度範囲の標準試料で作成した検量線の2種類を使い分ければよいです。もしくは、低濃度範囲と高濃度範囲のプロットが一つの二次曲線（や指数関数の曲線）で近似できるなら、その曲線で検量線をつくればよいです。曲線を数式化するには、エクセルの図にプロットして、近似曲線を描く機能を使います。

      注意事項：　曲線近似の場合、少しのずれが大きな誤差を生むことに注意してください。くれぐれも標準試料の濃度範囲内に未知試料の濃度が収まるようにしなくてはなりません。標準試料のプロットが、エクセルで表示した近似曲線上に乗っていることを確認するのを忘れずに。しばしば、全然違うところにプロットされたり、酷いときは二次曲線の頂点が検量線の定量範囲内に入ってしまうこともあります。


      ①は、「偶然誤差の許容範囲」つまり、測定精度の管理の問題です。測定精度とは、繰り返し測定をして、そのバラつき（標準偏差）がどれくらいかを表します。そのバラつきが、平均値に対してどれくらいの割合まで許容されるかを誤差として表します。

       

      以下、標準偏差と誤差の計算例です。


      測定項目xについて、繰り返し分析をi回行いました。平均、分散、標準偏差、誤差を以下のように計算します。

       

      平均値(ave)   ：1/n×Σxi                  (Σは、i=1～nの積算)

      分散(S)         ：1/(n-1)×Σ(xi – ave)2

      標準偏差(σ) ：S0.5

      標準誤差       ：σ／ave

      標準誤差(%)  ：(σ／ave)×100

       

      分散や標準偏差については、関数電卓やエクセルの関数に組み込まれているので忘れても困りません。それでも一応、計算方法を確認しておきましょう。下の分散Sと標準偏差σの空欄に値を記してください。

      繰り返し測定の結果：20, 21, 20, 19, 20, 18, 21, 20, 19, 22

      ave = 20、       S =       、σ =       　、標準誤差 = 5.77 %

       

      上の測定結果を単純に10倍した結果を下に記します。

      繰り返し測定の結果（B）：200, 210, 200, 190, 200, 180, 210, 200, 190, 220

      ave = 200、      S =       、σ =       　、標準誤差 = 5.77 %

      先の結果を10倍に増幅した結果を比べると、aveは10倍、Sは100倍、σは10倍になっています。標準誤差は（A）と（B）で同じです。標準誤差の意味がなんとなくわかったでしょうか。


      　分析化学では、測定感度をあげるため、信号強度を増幅(amplitude)させることがあります。スピーカーの音量をアンプで増幅するのと同じです。ただし、信号（音声）とノイズ（雑音）を一緒に増幅させると、聴きやすさ（測定精度：誤差）は変わりません。

       

      　さて、①の「偶然誤差の許容範囲」に話を戻します。分析者が、標準誤差で何％までを許容範囲とするか定めます。例えば、標準誤差10%以内を有効と定めれば、先の（A）や（B）の結果は有効と判断されます。ただし、繰り返し測定回数(n)を記しておくのを忘れないように。未知試料に対して、毎回10回も繰り返し測定するのは現実的ではないから、標準試料を10回くらい測定して分析精度を保証することが多いです。ここで注意したいのは、低濃度や高濃度の範囲で分析結果にバラつきが大きくなる（精度が悪くなる）ことです。低濃度や高濃度の未知試料の測定精度を保証するならば、その濃度に近い標準試料の繰り返し測定を行い、誤差を調べておく必要があるでしょう。

       

      次ページの定量下限と定量上限の説明をしたあとに、演習問題に取り組んでもらいます。


      　なお、標準試料のプロットが曲線で近似されることは、分析上、何か問題が生じていることを示唆しています。その理由を考え対処して、分析技術の向上を図るべきです。