物質が持つエネルギーの内訳（化学反応前後の変化）

Diagrama de temas

• General

  Colapsar todo Expandir todo
  • 

    English URL

• 水素と酸素の反応前後のエネルギー変化（概要）
  • 　化学反応の前後で物質が持つエネルギーの内訳が変わります。これらの差が何を意味するのかを学んでください。

    
    

    　標準状態（25℃、1気圧）において、水素と酸素から水を生成する反応前後のエネルギーの内訳を下図に示します。

    
    

    　反応前（原形）は、H₂とO₂の二成分が存在して、それぞれの物質のエンタルピー（物質がもつ総エネルギー）をHH₂、HO₂と記しました。エンタルピーの内訳は、内部エネルギー(U)とPVです。ここで注意したいのは、このPは全圧（1気圧）ではなく、各成分の分圧です。各成分の分圧の合計（全圧）が標準状態では1気圧です。（柔らかいビニール袋に、水素ガスと酸素ガスを注入した状態を想像すればよい）

    　水素と酸素が同じ空間に存在するのだから、体積Vは両成分共通になります。内部エネルギーは、束縛エネルギーとヘルムホルツ自由エネルギーで分配されています。ヘルムホルツ自由エネルギー(F)とPVを合計したものが、ギブズエネルギー（G）です。

    　原形の合計エンタルピーは、【 HH₂＋HO₂ 】で表され、同様に、原形の合計ギブズエネルギーは、【 GH₂＋GO₂ 】で表されます。
    

    
    

    
    

    
    

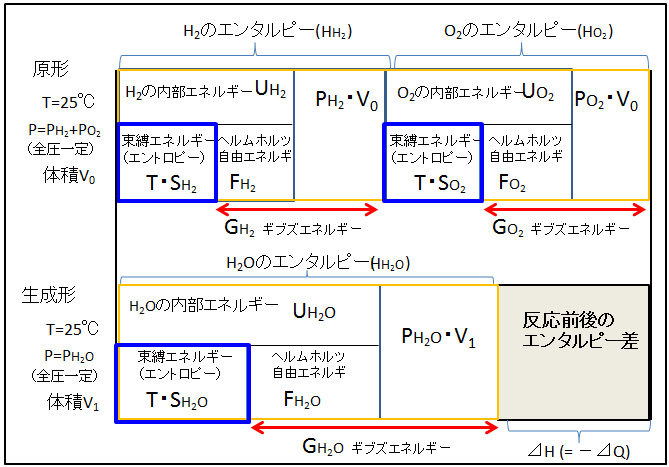
    　原形の水素と酸素が反応すると、水(H₂O)が生成されます。

    ・生成形の合計エンタルピー：HH₂O

    ・合計ギブズエネルギー：　　GH₂Oです。

    ・生成形と原形のギブズエネルギーの差（⊿G_{【生成形】－【原形】}）：　GH₂O－（GH₂＋GO₂）

    ・生成形と原形の束縛エネルギー差（T⊿S_{【生成形】－【原形】}）：　　　T・SH₂O－（T・SH₂＋T・SO₂）

    ・生成形と原形のエンタルピー差（⊿H_{【生成形】－【原形】}）：　　　　HH₂O－（HH₂＋HO₂）
    

    
    

    さて、原形と生成形の合計エンタルピーに違いが生じています。つまり、水素と酸素が反応して水になると、反応系の総エネルギーは減少してます。つまり、外界に熱として逃げているのです。⊿H_{【生成形】－【原形】}が熱量（⊿Q）に等しい。これが反応熱です。系からみると熱を失っているので、マイナス符号がつきます。
    

    
    

    
    

• 反応前後のエネルギー変化の式
  • 原形と生成形のエンタルピーを右辺に、その内訳を、束縛エネルギーとギブズエネルギーとして左辺に書きだしました。

     

                  原形：                T・S_水素＋G_水素＋T・S_酸素＋G_酸素　＝　H_水素＋H_酸素

                  生成形：            T・S_水＋G_水                    　　　　＝　H_水

     

    ここで、生成形と原形の両辺で差をとります（【生成形】－【原形】）

    T・S_水＋G_水 －（T・S_水素＋G_水素＋T・S_酸素＋G_酸素） ＝ H_水 －（H_水素＋H_酸素）

    これをまとめると、

    T⊿S_{【生成形】－【原形】}）＋ ⊿G_{【生成形】－【原形】} ＝ ⊿H_{【生成形】－【原形】}

    になります。

     

    
    

    ⊿H_{【生成形】－【原形】}＝T⊿S_{【生成形】－【原形】}）＋ ⊿G_{【生成形】－【原形】}

     

    これが意味するところは、化学反応前後の総エネルギー差（⊿H）が、

                  【物質の集合状態を調整するのに要する束縛エネルギー変化：T・⊿S】

                                                            と

                  【仕事として使える自由エネルギー差：⊿G】

    に分配されます。

     

     

    　さて、化学反応が進む向きや、化学平衡の条件を考えるとき、「エントロピー増大」の法則が登場する。

    
    

• 反応系と外界を含めたエントロピー、反応の進む向き
  • 　反応系の原形にはH₂とO₂、生成形にはH₂Oが存在します（下図）。生成形と原形を含めた反応系の束縛エネルギー変化は、T・⊿S_{【生成形】―【原形】}です（下図では、T・⊿S_系と表示）。　この反応が起こると、反応熱（⊿Q）が外界に伝わります。外界を含めて考えると、外界は熱⊿Qをうけとっているので、外界のエントロピーは⊿Q／T増えました。　ただし、外界は十分に大きく、反応前後で外界を含めた温度Tは変わりません。
    

    
    

    
    

    
    

    反応系と外界を含めた全体のエントロピー変化を⊿S_全体とすると、

     

    ⊿S_全体　＝　⊿S_{【生成形】-【原形】} + ⊿Q／T

     

    が成り立つ。この外界を含めた系は十分大きくて温度変化がないので、断熱系とみなせる。つまり、この系では、エントロピーが増大（S_全体＞0 ）するのです。
    

    
    

    
    エントロピー増大の条件を課すと、

     

    ⊿S_全体　＝　⊿S_{【生成形】-【原形】} + ⊿Q／T ＞ 0   ①

     

    これに、先に求めた以下の式を代入する。

     

    ⊿H_{【生成形】－【原形】}＝T⊿S_{【生成形】－【原形】}＋ ⊿G_{【生成形】－【原形】}

                  →　T⊿S_{【生成形】－【原形】}＝⊿H_{【生成形】－【原形】}－ ⊿G_{【生成形】－【原形】}

                  →　⊿S_{【生成形】－【原形】}＝⊿H_{【生成形】－【原形】}／T－ ⊿G_{【生成形】－【原形】}／T

    ①の⊿Sに代入

    ⊿H_{【生成形】－【原形】}／T  － ⊿G_{【生成形】－【原形】}／T  ＋⊿Q／T ＞ 0              ②

     

    エンタルピー変化と反応熱（-⊿Q）が等しく(⊿H_{【生成形】－【原形】}＝－⊿Q)、T>0なので、

    （－⊿Qのマイナス符号は、系からみると熱を失っているから。）

    
    

    ②は、⊿H_{【生成形】－【原形】}／T  － ⊿G_{【生成形】－【原形】}／T  －⊿H_{【生成形】－【原形】}／T ＞ 0

     

                  －⊿G_{【生成形】－【原形】}＞ 0

     

    つまり、

                  ⊿G_{【生成形】－【原形】}＜ 0　の向きに反応が進む

    
    

    化学反応が平衡にある条件とは、反応系と外界を含めたエントロピーが変化しない場合である。つまり、以下の条件が成り立ちます。

     

    ⊿G_{【生成形】－【原形】}＝ 0　

     

    
    

    次のコースでは、この条件式と熱力学関数を合わせて、先に扱った、化学平衡の条件式を導きます。