物質が持つエネルギーの内訳（はじめに）

Ringkasan topik

• Umum

  Ciutkan semua Perluas semua
  • 

    English URL
  • はじめに

    　化学平衡の基本式を理解するには、熱力学の知識が必要になります。水産学部の海洋生物科学科の学生には、物理化学や熱力学はあまり馴染みがないかもしれません。しかし、生物の代謝やエネルギー獲得を考えるうえで、その基礎になるのが熱力学である。例えば、生物の酸素呼吸によって有機物１モルから得られるエネルギーは？　酸素が無くて、嫌気的な環境で硝酸呼吸になると、どれだけエネルギー効率が悪くなるのか？　嫌気的な環境での生存戦略って、面白そう。そもそも酸化的とか嫌気（還元）的ってなに？　熱力学の基礎を知っていれば、これらの問いに計算で答えることができます。

    　「化学」と名のつく教科書（“分析化学”や“水圏化学”など）では、その第一章にて自由エネルギーやエンタルピーといったワードに出くわしてしまいます。真面目な学生ほど、教科書を１ページ目から読んで、基礎事項をクリアして先に進もうとします。しかし、分析化学や水圏化学の教科書を読むだけでは、これら基礎事項を理解するのは到底無理なのです。そうして1ページ目で挫折してしまう。

    　要領よく先に進みたい人は、化学平衡の条件式、電気化学の基本式だけ覚えて使いこなせればよいです。真面目だけど不器用な人は、遠回りだけれど、物理化学の基礎を理解したうえで先に進む道を選びましょう。

    
    

• 物質がもつ熱力学的なエネルギーの内訳
  • 熱力学的なエネルギー

    　熱力学的な“エネルギー”には、自由エネルギーと束縛エネルギーがあります。

    　前者の“自由エネルギー”とは、化学結合を組んだり、物質間で電子を移動させたり、体積を膨張させたり、このような仕事に使うことができるエネルギーのことです。

    　後者は、仕事につかえないエネルギーです。

     

    　エネルギーは熱力学関数（状態量：温度、圧力、体積、エントロピー^＊を使った関数）で表すことができ、そこから、化学反応の進む向き、反応の平衡条件、反応により生ずる熱、酸化還元反応により生ずる電位などが求められます。

    　化学実験を行うときは、反応前後の温度を一定に保ち、全圧を大気圧一定とするように、理想的な条件に設定できます。この理想的な条件のもと、ギブズの自由エネルギーを定義すると、計算が便利になるのです。

    ＊　熱力学関数の変形やエントロピーについては、のちほど詳しく説明します
    

  • 　いきなりですが、ギブズエネルギーの使い勝手と、その簡単な計算に慣れてもらいます。

    　化学反応では、物質（A）が持つ自由エネルギーを使って、化学結合を組みなおして、別の物質（B）が生成されます。化学反応を定量的に理解するため、物質（A）と（B）のエネルギー差を計算したり、物質がもつエネルギーの内訳を考えたりします。

    
    

    　まず、物質が持つ総エネルギーをエンタルピーと呼びます。それには、仕事につかえるエネルギー（自由エネルギー）と仕事に使えないエネルギー（束縛エネルギー）があります。

    
    

    【物質が持つ総エネルギー：エンタルピー】　＝

    　　　【仕事に使えるエネルギー：ギブズ自由エネルギー】

    　　　　　　　　　　＋　【仕事に使えないエネルギー：束縛エネルギー】

    
    

    　自由エネルギーにもいくつか種類があるのですが、ここではギブズ自由エネルギーを扱います。

    　ある物質のギブズ（自由）エネルギーとは、構成元素からその物質を合成するのに必要なエネルギーです。その物質をどれくらいの濃度でつくるのか、温度によっても必要なエネルギーは異なるので、以下のように定義します。

    
    

    元素A, B, C,,,,で構成される物質(ABC,,,)について、

    【ある状態の（任意の状態にある）物質（ABC,,,）のギブズ自由エネルギー】＝

    【標準状態（25℃, 1気圧）において、構成元素A, B, C,,,から物質（ABC,,,）を1mol合成するのに要するエネルギー】

    　　　　　　　　　　　　＋

    【標準状態にある物質（ABC,,,）から、任意の状態（異なる量（圧力・濃度）や温度）に変化させるのに要するエネルギー】

    
    

    右辺第一項：　標準状態（25℃, 1気圧）において、構成元素A, B, C,,,から物質（ABC,,,）1molを合成するのに要するエネルギーのことを、物質(ABC,,,)の標準生成ギブズエネルギーといいます。

    
    

    もう少し丁寧に標準生成ギブズエネルギーを説明：　　標準状態（25℃、1気圧）において、ある元素が単体で安定に存在する状態を基底（自由エネルギーゼロ）として、その単体（自由エネルギーゼロ）から物質を合成するのに要する自由エネルギーのことです。エネルギーの高低を論じるときは、どこかを基底（ゼロ）に定めなくてはならないので、標準状態で単体として安定に存在するときの各元素の自由エネルギーをゼロと定めました。水溶液中のイオン成分については、H⁺の標準生成ギブズエネルギーをゼロと定めています。

    
    

    なにやら、わけわからないでしょうが、例題を解いて慣れてゆきましょう

    
    

    【例題】　水素分子(H₂)と酸素分子(O₂)から水分子(H₂O)が生成されるときの、物質に含まれるエネルギーの内訳を示す。下図を軽く眺めてから、下にスクロールしてすすんでください。
    

    
    

    
    

    
    

    
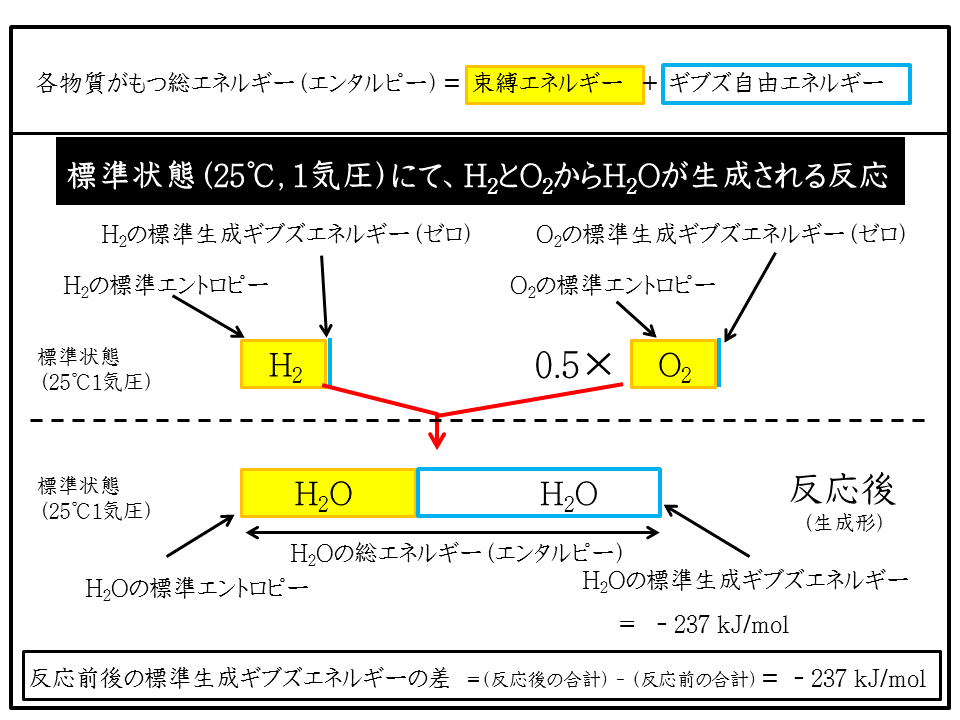
    　水分子（H₂O）であれば、構成する元素は水素(H)と酸素(O)です。それぞれの元素が単体で安定にある状態は、水素分子(H₂)と酸素分子(O₂)です。したがって、反応前の水素分子(H₂)と酸素分子(O₂)の標準生成ギブズエネルギーはともにゼロです。標準状態において、H₂とO₂が反応して1molのH₂Oを生成するのに要する自由エネルギーがH₂O(液体)の標準生成ギブズエネルギーで－237 (kJ/mol)です。

    　上の絵や先に説明したように、ある物質がもつ総エネルギーをエンタルピーと呼び、その内訳として、仕事として取り出せない「束縛エネルギー（エントロピー）」と仕事として取り出し得る「ギブズ自由エネルギー」があります。

    　そして、反応前後のギブズエネルギーの合計差が化学結合を組み直すのに使われるのです。

    （反応前後の総エンタルピーの差が、反応熱として外界に放出される。これについても、あとで詳しく説明する）

     

    （ちなみに、束縛エネルギー（エントロピー×温度）は物質の集合状態を表すエネルギーで、絶対零度のときに、理論上、各物質の束縛エネルギーがゼロになります。したがって、標準状態（25℃）にある物質の束縛エネルギーをゼロとは定めません。　上の絵にあるように、標準状態で安定に存在する単体であっても束縛エネルギーは存在し、そのとき（標準状態）のエントロピーを標準エントロピーと呼びます。各物質について、標準生成ギブズエネルギーと標準エントロピーの値が化学便覧などでまとめられています。　また、標準生成エントロピーとは、前項絵において、反応後のH₂Oの標準エントロピーから、反応前の単体（O₂とH₂）の標準エントロピーを差し引いたものです。　今の段階では、エントロピーについては理解しなくてもよいです。あとのコースで説明します。）

     

    　「こんなの、生物には関係ないっしょ、メンドクセー」という声が聴こえてきます。次のコースにて、標準生成ギブズエネルギーを使って、生物が呼吸によって得られるエネルギーを簡単に計算してみましょう。