海洋基礎生産のモデル計算（解析課題）
토픽 개요
-
-
海洋基礎生産の一次元モデル （難易度★★★）
以下の説明と問題１）～３）に従って、基礎生産モデルの解析に挑戦してください。
（下へスクロールすると、計算例のエクセルシートをダウンロードできます）
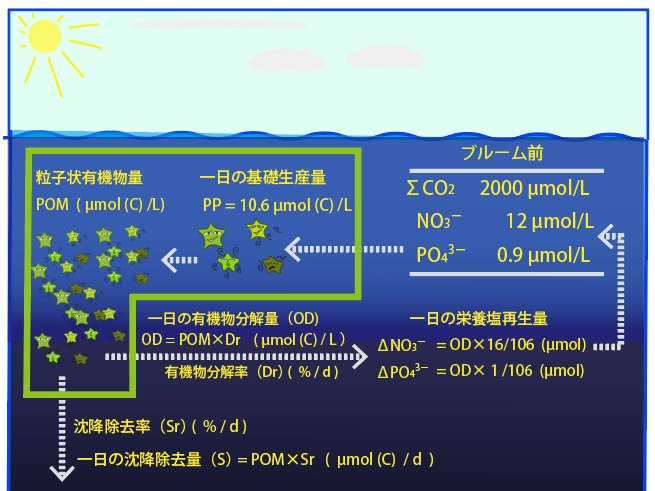
以下に、岸先生グループの海洋生態系モデルの研究論文を紹介します。植物プランクトンのブルームが起きる前の海水中の全炭酸と栄養塩の濃度が以下の通りでした。
全炭酸：2000 μmol/L、 NO3- : 12 μmol/L、 PO43- : 0.9 µmol/L
この海水で植物プランクトンブルームが起きて、基礎生産により有機炭素が 10.6 μmol (C) /L/d の速度で作られました。
NとPは、レッドフィールド比（C:N:P = 106:16:1）に等しく有機物に取り込まれるとします。
問題１）： NO3-かPO43-のどちらかが枯渇するまで、基礎生産が起こる場合、何日後に基礎生産はストップするでしょうか。
問題２）： 植物プランクトンブルームにより生産された有機物粒子のうち、毎日５～50 %（=Dr）が表層で分解され栄養塩が海水に再生します（この栄養塩は、再び表層で基礎生産に使われます）。同じく、毎日5～20%（=Sr）が表層混合層から沈降除去されて消失します。何日後に、表層で栄養塩が枯渇してブルームが終了するでしょうか？ 各自で好きなようにDrやSrの値を変化させて、いくつかの条件において、答えてください。
有機物分解率Dr（％ / d）：有機物粒子の分解・栄養塩再生率（5～50%）
沈降除去率Sr（％ / d） ：有機物粒子の沈降除去率（5～20%）
とすれば、
一日あたりの有機物分解量 (µmol/L）＝POM (µmol/L）×Dr (％/d）
一日あたりの有機物沈降除去量 (µmol/L）＝POM (µmol/L）×Sr (％/d）
になります。
ある日（d1）のPOM量を [POM]d1とすれば、次の日（d2）の [POM]d2 は、以下の式になります。
[POM]d2 = 10.6 μmol /L + [POM]d1 － [POM]d1×Dr － [POM]d1×Sr
（ただし、d1にて、基礎生産に必要な栄養塩が海水に存在する場合、10.6 μmol /Lが加わる）
ある日（d1）と次の日(d2）の栄養塩濃度も同様に記すと、
[NO3-]d2 = [NO3-]d1 - 10.6 ×16/106 + [POM]d1×Dr×16/106
[PO43-]d2 = [PO43-]d1 - 10.6 ×1/106 + [POM]d1×Dr×1/106
右辺第二項は、基礎生産で消費される栄養塩で、レッドフィールド比に従うことを想定して、16/106や1/106を乗じています。
右辺第三項は、現存する有機物量に比例（分解率Dr）して分解・再生される栄養塩です。これもレッドフィールド比に従うことを想定しました。
DrやSrを変化させて、ブルームが持続する期間に与える影響を考えてください。計算するエクセルシートの例をダウンロードして利用しても構いません。グラフや表を作るなど、工夫するとよいでしょう。
問題３） 余力があれば、様々な状況を追加で定めてみてください。
① 上の問題では、基礎生産速度（PP）を10.6 μmol (C)/L /dの一定値を与えてしまいました。PPは、現存する植物プランクトンの数に大きく依存します。ブルーム発生前にタネとして存在する植物プランクトン量を、例えばPOM = 0.1 μmol (C)/L とします。そして、POM量に比例した基礎生産速度を与えます。その比例定数（一日あたり、単位POMの基礎生産速度）をPr （単位： 1/d）として、例えば、Pr = 1～5 (1/d) の値を与えてみてはどうでしょうか。Pr = 5 とすれば、モデル計算1日目では、PP (μmol (C)/L /d) ＝ 0.1 (μmol (C)/L ) ×Pr (1/d) = 0.5 (μmol (C)/L /d) ですが、3日もすれば10.6 μmol (C)/L を超えてオーバーシュートの状態になるでしょう。実際の海洋では、初春に植物プランクトンの増加が見られてから、２～４週間後にブルームのピークを迎えることがあります。
② 基礎生産によるNとPの取り込み比率を変化させる。栄養塩が豊富にあれば、N/P比＝10 で取り込まれるとします。（対数増殖期のN/ P = 8.2 から、平均値のN/P = 16 まで取り得るので、仮に10としました） 栄養塩が豊富の状態として、NO3- > 1 μmol/L、PO43- > 0.5 μmol/L を与えてもよいでしょう。基礎生産が著しく制限を受ける栄養塩濃度として、仮に、NO3- < 0.1 μmol/L、PO43- < 0.05 μmol/L を与えるとよいです。栄養塩がこの濃度に達したら、基礎生産がストップすると考えてよいです。場合によっては、ブルームによる基礎生産が一旦ストップしても、表層海水に蓄えられた有機物粒子が分解して、緩やかな基礎生産が起こり続けることもあります。（実際の海洋でも、このようなことが見られます）
③ ①と②を組み合わせたうえで、栄養塩が少ない状況（基礎生産が著しく制限を受ける濃度～その濃度の2倍）では、基礎生産速度PPを、通常の1/10に低くする。
以下、レポート課題で取り組むのはハードルが高すぎると思われます。
④ 表層からの沈降除去率を変化させる。動物プランクトンによる捕食率、同化率、排泄率、糞粒の沈降除去率、などを与える。
⑤ 混合層の深さを考える。光の透過深度の変化を考える。夜と昼を設ける、、（これは難題になります）
⑥ 栄養塩成分のケイ素（Si）を加えて、植物プランクトンの種類を珪藻類（Siを必要とする）と渦鞭毛藻類（Siは不要）を設定する。栄養豊富な状態では珪藻の増殖速度を大きいことを想定する。
⑦ 大型捕食者を考える、、、、
基礎生産速度（PP）の見積もり 上の計算では、PP=10.6 μmol (c) /L/d を与えました。北海道噴火湾の珪藻による春季ブルーム期（3～4月: 49days）の平均値として、9.4 μmol (c) /L/d （= 5.5 g C/m3/49d; Table 2 of Maita and Odate, 1988）が報告されています。ブルーム開始から、終了までの全期間の平均値です。PP=10.6 μmol (c) /L/d は妥当な値だと思われます。
参考として、噴火湾表層における、ブルーム前から後までのクロロフィル(Chla）濃度、粒子状有機炭素（POC）濃度（クロロフィル濃度から概算）、リン酸（PO4）、硝酸（NO3）濃度を下にまとめました。
chla
(µg/L)POC
(µmol (C)/L)PO4
(µmol/L)NO3
(µmol/L)2019.2.15 0.78 2.3 0.88 9.1 3.4 21 63 0.39 0.28 3.15 11 33 0.36 0.78 4.14 0.19 0.57 0.31 0.05 5.12 0.41 1.23 0.1 0.05 上の表では、有機炭素濃度（OC (µmol (C) /L ) = 3×chla (µg/L) ）をかなり大雑把な方法で算出しました。
（北太平洋亜寒帯西部で行われた鉄散布実験の結果報告で読み取られた 3～4の値を参照）
2019年噴火湾では、硝酸枯渇によってブルームが終わることが考えられます。ブルームが終焉した４月のあと、5月にchla濃度が上昇しています。これは再生生産で説明できるでしょうか？ 再生生産で説明できるとすれば、どのようなモデルパラメタの値を設定する必要があるでしょうか。このような操作を、モデルパラメタのチューニングといいます。現実的なチューニングで説明できないなら、別の要因（外部からの栄養塩供給など）を考える必要があるでしょう。これらを突き詰めるのが、実際の研究現場で使われている「海洋生態系モデル」です。
（条件はいくらでも加えられます。疲れたら、途中でやめてくださいね）
北太平洋亜寒帯域における基礎生産と二次生産（餌生物となる動物プランクトン）をモデル解析して、サケの回遊場所や成長履歴までを解析する研究があります。温暖化による影響も解析されます。以下は、北大水産学部名誉教授の岸先生グループの研究成果です。現在は、同学部海洋資源科学科の上野先生が引き継いでいます。物理系の研究者が、海洋生物・化学をモデル解析しているのです。
-
海洋生態系モデル（北太平洋亜寒帯版：NEMURO）を使った、日本系サケの成長や分布を解析した研究です。ダウンロードサイトから全文（PDF）を入手してください。
-
例として、計算シートを配布します。計算方法を自由に書き換えて、モデル計算を試してください。
-