Derive a conditional equation for chemical equilibrium

主題大綱

• 一般

  全部收合 展開全部
  • 

    Japanese 網址

• "Enthalpy change" of the entire system = "Heat flow in and out".
  • The first law of thermodynamics is again noted.

    
    

    ⊿Q ＝ ⊿U ＋ P⊿V

    →　Considering the minute changes, dQ = dU + PdV   （１）

     

    The enthalpy (H) is defined as H = U + PV.

    The enthalpy of a substance means the total energy it possesses.

                                                                                                                   
    

    【Enthalpy (total energy)】＝【Internal energy (total kinetic energy of molecules)】

                                                     　　　 ＋【Energy (pressure x volume) that can be extracted by work to the outside world】

     

    Consider a small change in the enthalpy of the entire system.

    A minute change in enthalpy is expressed as follows

    dH = d(U + PV) = dU + PdV + VdP

    Since chemical experiments are performed at constant total pressure (atmospheric pressure), dP = 0, i.e.,
    
    　　dH = dU + PdV (2).

     

    Thus, from (1) and (2),

    dQ = dH　

    Therefore, the enthalpy change of the entire system before and after the chemical reaction (∆H) is equal to the heat in and out (∆Q) from the chemical reaction.

     

    　When describing heat transfer, is the system losing heat and giving a "minus sign" or is the outside world receiving heat from the system and giving a "plus sign"? These are the same phenomena, but it is easy to get confused about whether to put a positive or negative value on them. When describing the first law of thermodynamics (ΔQ = ΔU + PΔV), +ΔQ is the case where the system receives heat.
    

• Derivation of the conditional equation of chemical equilibrium
  • Derivation of the conditional equation of chemical equilibrium

     

    The condition under which a chemical reaction is in equilibrium is when the entropy of the reacting system, including the reacting system and the outside world, does not change. In other words, the following conditions hold

     

    ⊿G_{【product】－【original form】}＝ 0　

     

    From this condition,

    Conditional equation for chemical equilibrium：

    ⊿∑G_f⁰ = －RT・Ln{(Concentration product of product form) / (Concentration product of the original form)}

    We want to derive this. We will therefore deform the thermodynamic function.

    
    

    Review the energy breakdown diagram from the previous course (reaction between hydrogen and oxygen) to see that the following relationship holds

    G = U – TS + PV              (eq.1)

    The amount of this minute change is noted.

    dG = dU －TdS－SdT + PdV + VdP                        （eq.1-1）

     

    The first law of thermodynamics is written in terms of minute changes.

    dQ = dU + PdV

    
    

    The definition of entropy change is written in terms of minute changes：

    dS = dQ/T

    Multiply both sides of this by T

    →    TdS = dQ = dU + PdV             Substitute this into (Equation 1-1).

    dG = dU －(dU + PdV)－SdT + PdV + VdP = －SdT + VdP

    
    

    If the temperature is kept constant before and after the chemical reaction, dT = 0,

    dG = VdP

    From the equation of state of gas: PV = RT (at 1 mole),

    dG = RT/P dP

    This is then put into integral form.
    

    ∫dG = RT∫(1/P) dP

     

    If we integrate this from "partial pressure 1 in standard state" to "partial pressure P in any state",

    G_any －G_standard = RT・Ln(P_any／1) = RT・Ln(P_any)

    
    

    This G_standard is the standard generated Gibbs energy G_f⁰ that has emerged so far.In other words,
    

    G_any  = G_f⁰ + RT・Ln(P_any／1) = RT・Ln(P_any)

    
    

    As mentioned earlier, we assumed per mole in the equation of state of the gas, so what this equation means is the Gibbs energy per mole.

    In chemistry, the "Gibbs energy per mole" is called the chemical potential.

     

    Now consider a simple reaction system (substance A ⇆ substance B). The standard Gibbs energy of formation is noted below the reaction equation below.

    
    

                                                                          Origin form                       Generative form

                                                                          Substance A          ⇆        SubstanceB

    The standard Gibbs energy of formation      G_f⁰_{(A)generation}                          G_f⁰_(B)origin

     

    For substance A, the energy required to change from the standard state to an arbitrary concentration (partial pressure) and temperature is  RTLnP_A. 

    The Gibbs energy for an arbitrary state is expressed as

    Gibbs Energy in its original form：    G_(A)origin = G_f⁰_(A)origin + RT・LnP_A

    Gibbs energy in generative form：    G_(B)origin = G_f⁰_(B)origin + RT・LnP_B

     

    Conditions of equilibrium between the generated and original forms：⊿G = G_{(B)generation} － G_(A)origin = 0

    ∴G_f⁰_{(B)generation} + RT・LnP_B －(G_f⁰_(A)origin + RT・LnP_A) = 0

    
    

    A variant of this equation is,

    G_f⁰_{(B)generation} － G_f⁰_(A)origin =  RTLnP_A － RTLnP_B = －RT・Ln(P_B / P_A)

    
    

    This should be obtained,
    

    ⊿∑G_f⁰ = －RT・Ln{(concentration product of the generated form) / (concentration product of the original form)}

    　Here we have only considered one substance each in its original and product form, but it is the same if there is more than one. Let's also write down the chemical potential in μ and develop the equation in more detail.

    
    
    

  • Do the same derivation of the equation again, using the chemical potential (µ).

    
    

    Return to the earlier starting point.

    dG = (nRT/P)dP

    Integrate this to calculate the change in Gibbs energy when n moles of a substance are changed from state (0) to state (1).

     

    State (0): partial pressure P₀, temperature T₀

    State (1): partial pressure P₁, temperature T₀ (constant)

     

    ⊿G = G₁ – G₀ = nRT・  = nRT・Ln(P₁/P₀)

     

    Let state (0) be the standard state and P₀ = 1 atm, assuming that the system contains only the substance concerned.

    The change in Gibbs energy (⊿G) when changing from the standard state (0) to state (1) (partial pressure P₁) is expressed as follows

     

    ⊿G = G₁ － G₀ = nRT・LnP₁

     

    The Gibbs energy per mole is called the chemical potential (μ).

     

    ⊿μ = μ₁ – μ₀ = RT・LnP₁

     

    (In chemistry, the Gibbs energy per mole is called the chemical potential; in physics, the Gibbs energy per particle is called the chemical potential.)

     

    By convention, the subscript "0" represents the standard state. The subscript "1" is omitted when representing an arbitrary state (arbitrary partial pressure P) at the destination of the change.

     

    In other words, the change in Gibbs energy when one mole of a substance goes from the standard state to pressure P can be expressed using the chemical potential as follows.

     

     μ – μ₀ = RT・LnP

      →   μ = μ₀ + RT・LnP

     

    This formula means

    【Gibbs energy for one mole of a substance at pressure P】

    ＝【Gibbs energy for one mole of that substance in its standard state】

     ＋【Gibbs energy change when the substance changes from its standard state to pressure P】

    
    

    (This μ₀ is the standard generated Gibbs energy.)

     

    Consider a chemical reaction (original form before the reaction, production form after the reaction).

     

    Original form 【Substance Q in q moles and partial pressure P_Q, substance R in r moles and partial pressure P_R, substance S in s moles and ...】

    These substances react to,

     Production form【Substance X is x moles and partial pressure P_x, substance Y is y moles and partial pressure P_Y, substance Z is z moles ...】

    
    

     

    Gives energy of each substance in its original form

                  Substance Q ： G_Q = q・(μ_Q⁰   +   RT・lnP_Q )

                  Substance R ： G_R = r・(μ_R⁰   +   RT・lnP_R )

                  Substance S ： G_S = s・(μ_S⁰   +   RT・lnP_S )

                  ...

     

    Gives energy for each substance in its production form

                  Substance X ： G_X = x・(μ_X⁰   +   RT・lnP_x )

                  Substance Y ： G_Y = y・(μ_Y⁰   +   RT・lnP_Y )

                  Substance Z ： G_Z = z・(μ_Z⁰   +   RT・lnP_Z )

                  ...

    
    
    
    
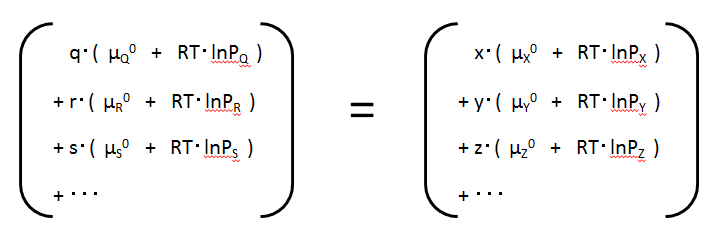
    　In this equation, for each substance, the chemical potential of the standard state is summarised on the left-hand side and the term for the change in Gibbs energy when changing from the standard state to any state (original or production form) on the right-hand side.
    
    
    

    原形の標準生成ギブズエネルギーの合計Total standard generated Gibbs energy of the original form.

    生成形の標準生成ギブズエネルギーの合計Total standard generating Gibbs energy of the production form.
    

    
    

    　The "standard state chemical potential" of each substance, summarised on the left-hand side, is equal to the "standard production Gibbs energy" of each substance. We write this as G_f⁰, which is an acronym for formation. (Note that the abbreviation varies from book to book.)

     

    The above equation for the equilibrium condition can be summarised as,

    
    
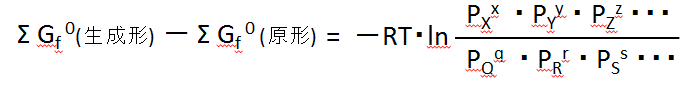
    生成形production form 原形Original form
    
    This was noted earlier,
    
    
    生成形の濃度積 concentration product of production form
    

    
    

    原形の濃度積 concentration product of original form
    
    

    
    
    

  • 
    

    
    

    【Supplement】

    　What's that?　It is the 'partial pressure' of each substance that goes into the equilibrium constant K, is it not?　Why can I also use it as a proxy for molar concentration in solution chemistry?　You may wonder.

     

    　In solution chemistry, we consider the standard Gibbs energy of formation (G_f⁰) of an ion dissolved in water; since we cannot make a solution containing only one type of ion, the G_f⁰ of an ion is always relative. The G_f⁰G_f⁰ of the hydrogen ion H+ in aqueous solution is defined as 0, while the G_f⁰ of the other ions is expressed as relative values. The reason there is no problem with relative values is that K is expressed as a ratio of concentration product/concentration product.

    　Therefore, '⊿G_f⁰ ＝ －R・T・lnK' can be applied directly to solution chemistry.

    
    

    　To be precise, the equilibrium constant K is not expressed in terms of the concentration or partial pressure of each substance, but K is expressed as a product of the 'active mass' of each substance. The active mass is the proportion of molecules that are active in a chemical reaction. To describe a "ratio", something must be set to 1. A more detailed explanation of active quantities will be given in the section "Ionic Strength and Debye Radius" next to Chemical Equilibrium. For now, remember that

     

    ・　The molar concentration a (mol/L) of the ideal solution is the active volume a.

    ・　The partial pressure b (atm) of an ideal gas is the active volume b.

    ・　The electron activity is set to 1.

    ・　When water molecules are involved in the reaction in aqueous solution, the water activity is set to 1.

    ・　When solids are present in a gas- or liquid-phase reaction, the activity of the solids is 1.

    ・　When a liquid is produced in a gas-phase reaction, the active volume of the liquid is 1.

     

    　In non-ideal (real) solutions and non-ideal (real) gases, not all substances of a certain concentration are involved in chemical reactions. In concentrated solutions and high-pressure gases, the proportion of substances that are not involved in chemical reactions and is larger.The coefficient to compensate for this ratio is called the activity coefficient. For the moment, it is only necessary to understand it in ideal conditions.