セクションアウトライン

  • 折りたたむ 展開する

    一般

    すべてを折りたたむ すべてを展開する
  • 折りたたむ 展開する

    "Enthalpy change" of the entire system = "Heat flow in and out".

    • The first law of thermodynamics is again noted.


      ⊿Q ＝ ⊿U ＋ P⊿V

      →　Considering the minute changes, dQ = dU + PdV   （１）

       

      The enthalpy (H) is defined as H = U + PV.

      The enthalpy of a substance means the total energy it possesses.

                                                                                                                     

      【Enthalpy (total energy)】＝【Internal energy (total kinetic energy of molecules)】

                                                       　　　 ＋【Energy (pressure x volume) that can be extracted by work to the outside world】

       

      Consider a small change in the enthalpy of the entire system.

      A minute change in enthalpy is expressed as follows

      dH = d(U + PV) = dU + PdV + VdP

      Since chemical experiments are performed at constant total pressure (atmospheric pressure), dP = 0, i.e.,

      　　dH = dU + PdV (2).

       

      Thus, from (1) and (2),

      dQ = dH　

      Therefore, the enthalpy change of the entire system before and after the chemical reaction (∆H) is equal to the heat in and out (∆Q) from the chemical reaction.

       

      　When describing heat transfer, is the system losing heat and giving a "minus sign" or is the outside world receiving heat from the system and giving a "plus sign"? These are the same phenomena, but it is easy to get confused about whether to put a positive or negative value on them. When describing the first law of thermodynamics (ΔQ = ΔU + PΔV), +ΔQ is the case where the system receives heat.

  • 折りたたむ 展開する

    Derivation of the conditional equation of chemical equilibrium

    • Derivation of the conditional equation of chemical equilibrium

       

      The condition under which a chemical reaction is in equilibrium is when the entropy of the reacting system, including the reacting system and the outside world, does not change. In other words, the following conditions hold

       

      ⊿G【product】－【original form】＝ 0　

       

      From this condition,

      Conditional equation for chemical equilibrium：

      ⊿∑Gf0 = －RT・Ln{(Concentration product of product form) / (Concentration product of the original form)}

      We want to derive this. We will therefore deform the thermodynamic function.


      Review the energy breakdown diagram from the previous course (reaction between hydrogen and oxygen) to see that the following relationship holds

      G = U – TS + PV              (eq.1)

      The amount of this minute change is noted.

      dG = dU －TdS－SdT + PdV + VdP                        （eq.1-1）

       

      The first law of thermodynamics is written in terms of minute changes.

      dQ = dU + PdV


      The definition of entropy change is written in terms of minute changes：

      dS = dQ/T

      Multiply both sides of this by T

      →    TdS = dQ = dU + PdV             Substitute this into (Equation 1-1).

      dG = dU －(dU + PdV)－SdT + PdV + VdP = －SdT + VdP


      If the temperature is kept constant before and after the chemical reaction, dT = 0,

      dG = VdP

      From the equation of state of gas: PV = RT (at 1 mole),

      dG = RT/P dP

      This is then put into integral form.

      ∫dG = RT∫(1/P) dP

       

      If we integrate this from "partial pressure 1 in standard state" to "partial pressure P in any state",

      Gany －Gstandard = RT・Ln(Pany／1) = RT・Ln(Pany)


      This Gstandard is the standard generated Gibbs energy Gf0 that has emerged so far.In other words,

      Gany  = Gf0 + RT・Ln(Pany／1) = RT・Ln(Pany)


      As mentioned earlier, we assumed per mole in the equation of state of the gas, so what this equation means is the Gibbs energy per mole.

      In chemistry, the "Gibbs energy per mole" is called the chemical potential.

       

      Now consider a simple reaction system (substance A ⇆ substance B). The standard Gibbs energy of formation is noted below the reaction equation below.


                                                                            Origin form                       Generative form

                                                                            Substance A          ⇆        SubstanceB

      The standard Gibbs energy of formation      Gf0(A)generation                          Gf0(B)origin

       

      For substance A, the energy required to change from the standard state to an arbitrary concentration (partial pressure) and temperature is  RTLnPA. 

      The Gibbs energy for an arbitrary state is expressed as

      Gibbs Energy in its original form：    G(A)origin = Gf0(A)origin + RT・LnPA

      Gibbs energy in generative form：    G(B)origin = Gf0(B)origin + RT・LnPB

       

      Conditions of equilibrium between the generated and original forms：⊿G = G(B)generation － G(A)origin = 0

      ∴Gf0(B)generation + RT・LnPB －(Gf0(A)origin + RT・LnPA) = 0


      A variant of this equation is,

      Gf0(B)generation － Gf0(A)origin =  RTLnPA － RTLnPB = －RT・Ln(PB / PA)


      This should be obtained,

      ⊿∑Gf0 = －RT・Ln{(concentration product of the generated form) / (concentration product of the original form)}

      　Here we have only considered one substance each in its original and product form, but it is the same if there is more than one. Let's also write down the chemical potential in μ and develop the equation in more detail.



    • Do the same derivation of the equation again, using the chemical potential (µ).


      Return to the earlier starting point.

      dG = (nRT/P)dP

      Integrate this to calculate the change in Gibbs energy when n moles of a substance are changed from state (0) to state (1).

       

      State (0): partial pressure P0, temperature T0

      State (1): partial pressure P1, temperature T0 (constant)

       

      ⊿G = G1 – G0 = nRT・  = nRT・Ln(P1/P0)

       

      Let state (0) be the standard state and P0 = 1 atm, assuming that the system contains only the substance concerned.

      The change in Gibbs energy (⊿G) when changing from the standard state (0) to state (1) (partial pressure P1) is expressed as follows

       

      ⊿G = G1 － G0 = nRT・LnP1

       

      The Gibbs energy per mole is called the chemical potential (μ).

       

      ⊿μ = μ1 – μ0 = RT・LnP1

       

      (In chemistry, the Gibbs energy per mole is called the chemical potential; in physics, the Gibbs energy per particle is called the chemical potential.)

       

      By convention, the subscript "0" represents the standard state. The subscript "1" is omitted when representing an arbitrary state (arbitrary partial pressure P) at the destination of the change.

       

      In other words, the change in Gibbs energy when one mole of a substance goes from the standard state to pressure P can be expressed using the chemical potential as follows.

       

       μ – μ0 = RT・LnP

        →   μ = μ0 + RT・LnP

       

      This formula means

      【Gibbs energy for one mole of a substance at pressure P】

      ＝【Gibbs energy for one mole of that substance in its standard state】

       ＋【Gibbs energy change when the substance changes from its standard state to pressure P】


      (This μ0 is the standard generated Gibbs energy.)

       

      Consider a chemical reaction (original form before the reaction, production form after the reaction).

       

      Original form 【Substance Q in q moles and partial pressure PQ, substance R in r moles and partial pressure PR, substance S in s moles and ...】

      These substances react to,

       Production form【Substance X is x moles and partial pressure Px, substance Y is y moles and partial pressure PY, substance Z is z moles ...】


       

      Gives energy of each substance in its original form

                    Substance Q ： GQ = q・(μQ0   +   RT・lnPQ )

                    Substance R ： GR = r・(μR0   +   RT・lnPR )

                    Substance S ： GS = s・(μS0   +   RT・lnPS )

                    ...

       

      Gives energy for each substance in its production form

                    Substance X ： GX = x・(μX0   +   RT・lnPx )

                    Substance Y ： GY = y・(μY0   +   RT・lnPY )

                    Substance Z ： GZ = z・(μZ0   +   RT・lnPZ )

                    ...





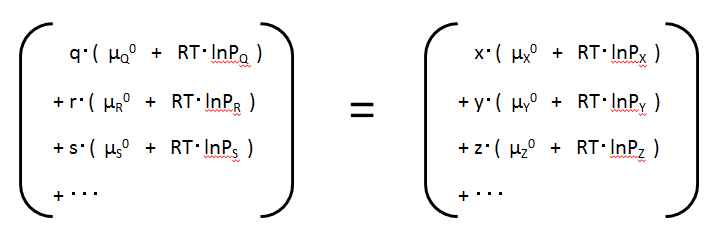
      　In this equation, for each substance, the chemical potential of the standard state is summarised on the left-hand side and the term for the change in Gibbs energy when changing from the standard state to any state (original or production form) on the right-hand side.


      原形の標準生成ギブズエネルギーの合計Total standard generated Gibbs energy of the original form.
      生成形の標準生成ギブズエネルギーの合計Total standard generating Gibbs energy of the production form.

      　The "standard state chemical potential" of each substance, summarised on the left-hand side, is equal to the "standard production Gibbs energy" of each substance. We write this as Gf0, which is an acronym for formation. (Note that the abbreviation varies from book to book.)

       

      The above equation for the equilibrium condition can be summarised as,



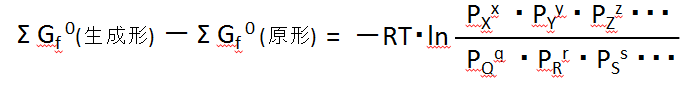
      生成形production form 原形Original form

      This was noted earlier,


      生成形の濃度積 concentration product of production form

      原形の濃度積 concentration product of original form





    • 【Supplement】

      　What's that?　It is the 'partial pressure' of each substance that goes into the equilibrium constant K, is it not?　Why can I also use it as a proxy for molar concentration in solution chemistry?　You may wonder.

       

      　In solution chemistry, we consider the standard Gibbs energy of formation (Gf0) of an ion dissolved in water; since we cannot make a solution containing only one type of ion, the Gf0 of an ion is always relative. The Gf0Gf0 of the hydrogen ion H+ in aqueous solution is defined as 0, while the Gf0 of the other ions is expressed as relative values. The reason there is no problem with relative values is that K is expressed as a ratio of concentration product/concentration product.

      　Therefore, '⊿Gf0 ＝ －R・T・lnK' can be applied directly to solution chemistry.


      　To be precise, the equilibrium constant K is not expressed in terms of the concentration or partial pressure of each substance, but K is expressed as a product of the 'active mass' of each substance. The active mass is the proportion of molecules that are active in a chemical reaction. To describe a "ratio", something must be set to 1. A more detailed explanation of active quantities will be given in the section "Ionic Strength and Debye Radius" next to Chemical Equilibrium. For now, remember that

       

      ・　The molar concentration a (mol/L) of the ideal solution is the active volume a.

      ・　The partial pressure b (atm) of an ideal gas is the active volume b.

      ・　The electron activity is set to 1.

      ・　When water molecules are involved in the reaction in aqueous solution, the water activity is set to 1.

      ・　When solids are present in a gas- or liquid-phase reaction, the activity of the solids is 1.

      ・　When a liquid is produced in a gas-phase reaction, the active volume of the liquid is 1.

       

      　In non-ideal (real) solutions and non-ideal (real) gases, not all substances of a certain concentration are involved in chemical reactions. In concentrated solutions and high-pressure gases, the proportion of substances that are not involved in chemical reactions and is larger.The coefficient to compensate for this ratio is called the activity coefficient. For the moment, it is only necessary to understand it in ideal conditions.