Mechanical Separation Operation
Garis besar topik
-
-
1-1．frequency distribution curve
Frequency of mass or volume of particles in a given particle size range.
The particle size with the greatest frequency is the 'mode diameter'.
1-2．Residual curves (R-curves, sieve top curves)
Fraction of the mass or volume of particles that 'remain' on a sieve of the same size as the particle size.
The particle size at which the residual is 50% is the 'median diameter'.
1-3．Passage rate curves (P-curves, under sieve curves)
Fraction of the mass or volume of particles that 'pass' through a sieve of the same size as the particle size.
Pass rate（P） = 1 – Residual（R）
残留率residual メディアン径median diameter 粒子径particle size 篩の目の大きさSieve size
1-4．Rosin-Rammler distribution
Empirical formula that fits well with the particle size distribution of actual powders and grain particles.
R = exp[-(D/De)ⁿ] (1-1)
D is the particle size, De is the particle size at 37% residual, the higher the n value the more uniform the particle size.
-
-
-
Equation of motion of a particle in a fluid (inertia force = gravity - buoyancy force - resistance force)
(2-1)CD coefficient of resistance of a fluid，D Particle diameter，t time，u particle settling velocity，ρ Fluid density，ρs Particle density
When fine particles are dropped into a fluid, they initially undergo an accelerated motion, which soon becomes a constant velocity motion (du/dt = 0). This is called the terminal velocity.
ut = ( ρs– ρ)gD²/18μ (2-2)
ut (m/s) terminal velocity，μ (Pa·s) Viscosity of fluid
The terminal velocity of particles is proportional to the density difference between the fluid and the particles, and proportional to the square of the particle diameter.
-
-
-
3-1．Andresen pipette method
The particle sizing operation using an Andresen pipette (see right) is very simple as follows.
1）Add a predetermined amount of liquid and powder to an Andresen pipette, stir well and allow to stand.
2）Sample liquid is collected at predetermined times with a pipette attached to the top and the concentration of solids is measured.
3）Usually, the concentration is determined by measuring the mass of solids remaining in the dried sample solution.
The mass of solids in the sample solution decreases with time. The reduced mass is equal to the mass of the group of particles with a settling velocity that can pass from the liquid surface to the pipette tip (distance H) during the time between standing still and taking the sample (time t).Therefore, the solid concentration C of the sample solution collected at time t divided by the initial concentration C0 corresponds to the proportion of the particle population with a terminal velocity slower than H/t (pass rate), and a pass rate curve can be drawn by converting the collection time into particle size using the Stokes formula (Equation 2-2).
-
3-2．sedimentation balance method
If a well-stirred suspension is placed in the settling tube shown on the bottom left and the change over time in the mass of solids deposited in the trap is measured, a graph (settling curve) like that shown on the bottom right can be obtained. If the grain size is uniform, the mass increases linearly; if it is non-uniform, it is non-linear. If the deposited weight at time t is Wt and the weight when the weight no longer changes is Wf, the residual rate R is
(3-1)Differentiating Equation 3-1 with respect to t yields
(3-2)From Equations 3-1 and 3-2, it follows that
(3-3)Once the density of the particles and the density and viscosity of the fluid are known, time can be converted to particle size by the Stokes equation. On the other hand, since the intercept of the tangent to the sedimentation curve is equal to the residual fraction R, from this result a residual fraction curve can be drawn.
電子天秤electronic balance 沈降管settling tube 堆積物の質量Mass of sediment 粒子が均一Particle uniformity 粒子の沈降速度Sedimentation rate of particles 粒子が不均一Particle non-uniformity 時間time
-
-
4-1．filtration
The basic equation (Lewis equation) is
(4-1)v（m/s） filtrate flux，A（m2） Filtration area，V（m3） filtrate volume，t（s） filtrate time，μ（kg/m·s）Fluid viscosity，ΔP（Pa） Filtration pressure, Rm Filter material (filter paper or membrane) resistance coefficient，Rc （m-1）Resistance coefficient of filtration (cakes, solids deposited on filter media).
The resistance coefficient of the filter media is constant if clogging does not occur during filtration operations. On the other hand, the cake resistance increases with the accumulation of solids on the filter media; if the cake is incompressible,
Rc = αCV/A (4-2)
α（m/kg）Cake resistivity，C（kg/m3） Concentration of solids in filtration stock solution
From Equations 4-1 and 4-2, it follows that
(4-3)On an industrial scale, 'constant speed filtration', in which the pressure is controlled to maintain a constant flow rate of filtrate, and 'constant pressure filtration', in which the pressure is kept constant, are used.
-
4-1-1．Constant speed filtration
Since dV/dt = V/t in constant velocity filtration
(4-4)Therefore, the ΔP vs. V plot for constant speed filtration is a straight line, and the slope gives the cake resistivity α and the intercept gives the filter media resistance coefficient Rm.
4-1-2．Constant pressure filtration
Since ΔP is constant in constant pressure filtration
(4-5)Equation 4-5 is called the Ruth equation. In constant pressure filtration, the plot of t/V vs. V is a straight line, and the slope gives the cake resistivity α and the intercept gives the filter media resistance coefficient Rm.
4-1-3．gravity filtration
Gravity filtration experiments often use "gravity filtration" with a filter paper and a funnel. In gravity filtration, the filtration pressure decreases in proportion to the filtrate volume, so
(4-6)ρ（kg/m3）Fluid density，g （m/s2） acceleration of gravity，h0 （m） Liquid depth of filtration stock solution，Av（m2） Filter cross-sectional area
Integrating Equations 4-6 from t = 0 to t and V = 0 to V
(4-7)In Equation 4-7, the values other than α are equipment specifications, operating conditions, and experimental results, so a plot with the left side of the above equation on the y-axis and the values other than α on the right side on the x-axis is a straight line, and α can be obtained from the slope. Also, since C = 0 when the filtrate contains no solids,
(4-8)Therefore, applying Equation 3-8 to the results of the water transmission experiment, Rm is obtained from the slope.
-
4-2．centrifuge
The centrifugal force F acting on an object of mass m moving with angular velocity ω (rad) on a circumference of radius r is
F = mrω² (4-9)
When the centrifuge is operating at number of rotations N, the distance L travelled in one second by an object at r from the center is
L = 2πrN (4-10)
In many centrifuge specifications, the number of revolutions is expressed in r.p.m. (revolution per minute). In international units, it should be converted to r.p.s. (revolutions per second).Since an angular velocity of 1 rad is the angle formed by a solitary body of the same length as the radius
ω = 2πrN/r = 2πN (4-11)
From Equations 4-9 and 4-11, we see that
F = 4mπ²N²r (4-12)
The ratio of the centrifugal force to the universal gravitation force mg in Equation 4-12 is the centrifugal effect x.
x = 4mπ²N²r /mg = 4π²N²r/g (4-13)
Usually, centrifugal force is denoted as 10 G or 100 G, where the number denotes the centrifugal effect x and G denotes the gravitational acceleration. Gravitational acceleration is denoted by a capital "G" to distinguish it from mass (g).
4π²N²r = xg ≡ xG (4-14)
Since the driving force for a particle settling in a fluid in a centrifugal field is centrifugal force, the gravitational acceleration in the Stokes equation is replaced by Equation 4-14,
(4-15)Since the centrifugal force is a function of the distance r from the center of the axis of rotation to the particle
ut = dr/dt (4-16)
From Equations 4-15 and 4-16, one can determine the time it takes for the particles to settle to the bottom of the centrifuge tube by centrifugation.
-
-
-
5-1．Electrostatic repulsive force between particles
5-1-1．Particle surface charge
The interfaces of solid and gas phases in contact with the liquid phase are often negatively charged. This is because cations are more easily hydrated and stabilized in the liquid phase. The surfaces of organic as well as inorganic materials are negatively charged above neutral pH. In the case of microorganisms, carboxyl and phosphate groups on the surface are negatively charged, while amino and imidazole groups are positively charged. Therefore, the entire surface has a negative charge in the alkaline range where the amino and imidazole groups lose their charge, and the entire surface has a positive charge at low pH where the carboxyl and phosphate groups lose their charge, creating an "electrostatic repulsive force" between like particles with the same surface charge.
5-1-2．electric double layer
Negatively charged solid surfaces attract cations. On the other hand, since fine particles in water are in Brownian motion, the positive charge near the particle surface has a diffuse distribution with a higher density the closer it is to the surface (Gouy-Chapman diffusion double-layer model).
Φ = Φ0 exp(-κL) (5-1)
Φ Potential at distance L from particle surface，Φ0 surface potential，κ Debye parameter
The distance L = 1/κ is called the "thickness of the electric double layer." As the liquid-phase ionic strength increases, 1/κ decreases. This is called the "compression of the electric double layer".
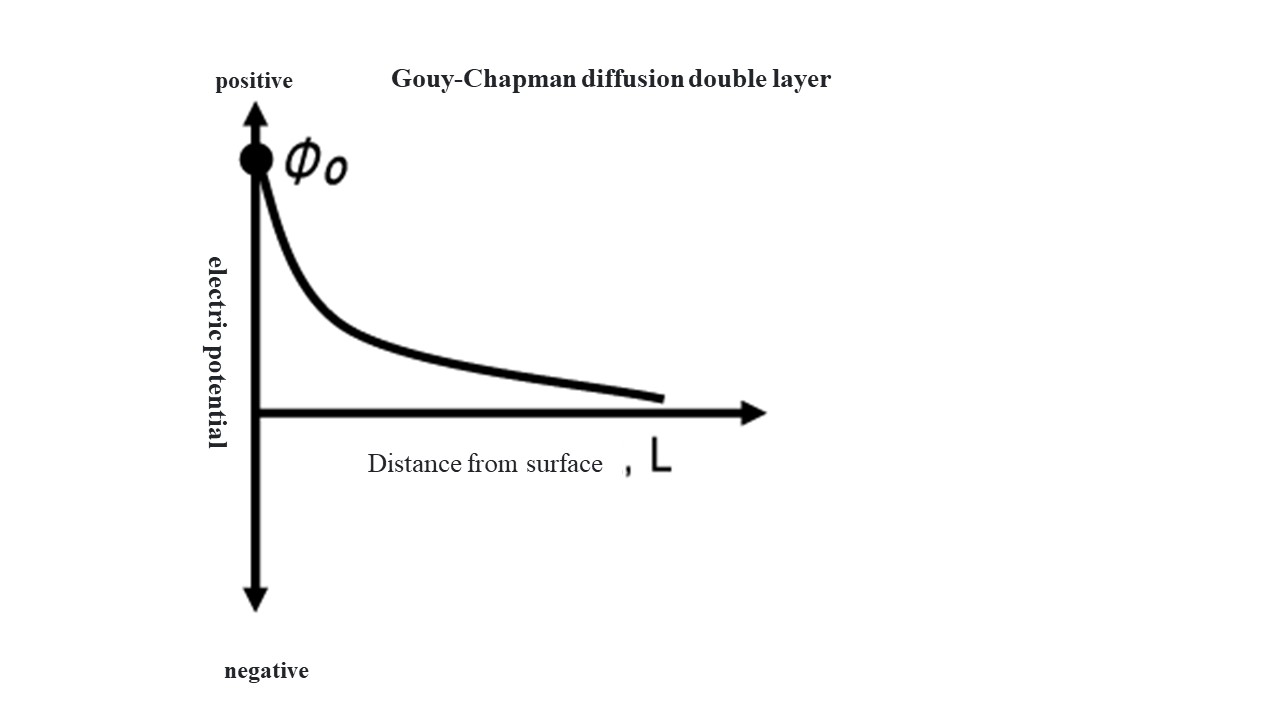
Gouy-Chapmanの拡散2重層Gouy-Chapman diffusion double layer 電位electric potential 正positive 負negative 表面からの距離Distance from surface
5-1-3．Repulsive force produced by the electric double layer
The electrostatic repulsive force VR acting between spherical particles of the same charge and size is
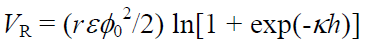(5-2)r Particle radius，h Distance between particles，ε Dielectric Constant of Liquid Phase
5-2．Attractive force between particles (van der Waals force)
The van der Waals forces of attraction act between the molecules that make up matter. van der Waals forces consist of the following three forces.
1）Interdipole attraction: Attractive force exerted by molecules with asymmetric electron distribution in a molecule as permanent dipoles.
2） Induced effect: Attractive force exerted by the polarization of a molecule adjacent to a molecule with a permanent dipole
3） London dispersion force: Universal intermolecular attraction between molecules with low polarity and no permanent dipole. It is a short-range attraction that is inversely proportional to the seventh power of the intermolecular distance, but in the case of colloidal size molecular aggregates it can be quite far-reaching.