Model calculation of Primary production in the sea (analysis task)
主题目录
-
-
One-dimensional model of primary production in the sea（Difficulty★★★）
Follow the instructions and Question 1) through 3) below to try to analyze the primary production model.
(Scroll down to download an Excel sheet with example calculations)
The concentrations of total carbonate and nutrients in seawater before the phytoplankton bloom occurred were as follows
Total carbonic acid：2000 μmol/L、 NO3- : 12 μmol/L、 PO43- : 0.9 µmol/L
A phytoplankton bloom occurred in this seawater and organic carbon was produced at a rate of 10.6 µmol (C)/L/d through primary production.
Assume that N and P are incorporated into organic matter at equal Redfield ratios (C:N:P = 106:16:1).
Question 1)： In the case that primary production continues until NO3- or PO43- is depleted, after how many days will basic production stop?
Question 2)： Of the organic particles produced by the phytoplankton bloom, 5-50 % (=Dr) are decomposed daily in the surface layer to regenerate nutrients in seawater (which are again used in the surface layer for primary production). Likewise, 5 to 20% (=Sr) is removed daily by settling out of the surface mixed layer. After how many days will the nutrient be depleted in the surface layer and the bloom end? Answer this question in several conditions, varying the values of Dr and Sr as desired by each person.
Assume
Organic decomposition rate Dr（％ / d）：Organic particle decomposition and remineralization rate（5～50%）
Sedimentation removal rate Sr（％ / d）：Sedimentation removal rate of organic particles（5～20%）
Then
Amount of organic matter decomposed per day (µmol/L）＝POM (µmol/L）×Dr (％/d）
Organic sedimentation and removal per day (µmol/L）＝POM (µmol/L）×Sr (％/d）
If the amount of POM on one day (d1) is [POM]d1, then [POM]d2 on the next day (d2) is given by
[POM]d2 = 10.6 μmol /L + [POM]d1 － [POM]d1×Dr － [POM]d1×Sr
(Note: at d1, if the nutrients necessary for primary production are present in seawater, 10.6 μmol /L is added)
The nutrient concentrations on one day (d1) and the next day (d2) would be noted in the same way,
[NO3-]d2 = [NO3-]d1 - 10.6 ×16/106 + [POM]d1×Dr×16/106
[PO43-]d2 = [PO43-]d1 - 10.6 ×1/106 + [POM]d1×Dr×1/106
The second term on the right-hand side is the nutrients consumed in primary production, multiplied by 16/106 or 1/106, assuming that the Redfield ratio is followed.
The third term on the right-hand side is the nutrients that are decomposed and regenerated in proportion to the amount of organic matter present (decomposition rate Dr). This was also assumed to follow the Redfield ratio.
Consider the effect of varying Dr and Sr on the duration of the bloom. You may download and use an example Excel sheet to do the calculations. You may want to make a graph or table.
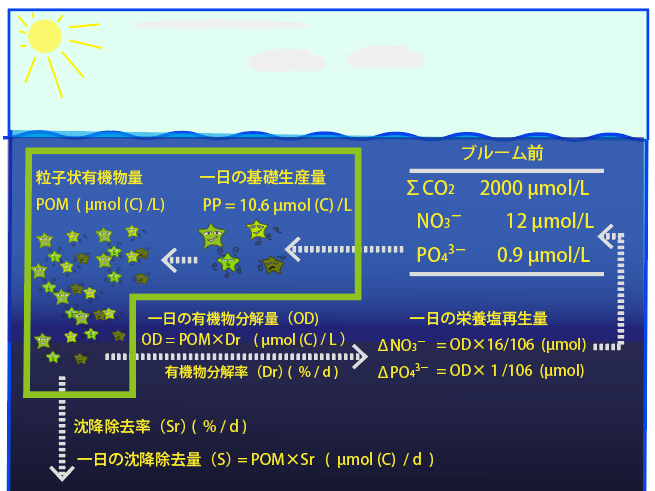
粒子状有機物量：Amount of particulate organic matter 一日の基礎生産量： Primary production rate ( /day) ブルーム前： Before blooming 一日の有機物分解量： Amount of organic decomposition (/day) 有機物分解率：Organic decomposition rate 一日の栄養塩再生量：Amount of remineralization (/day) 沈降除去率：Sedimentation removal rate 一日の沈降除去量：Amount of sedimentation removal (/day)
Question 3) If you have extra capacity, try to define additional various situations.
① In the above problem, we gave a constant value of 10.6 μmol (C)/L /d for the primary production rate (PP); PP is highly dependent on the number of phytoplankton present. Let the amount of phytoplankton present as seeds before the bloom occurs, for example, POM = 0.1 μmol (C)/L. Then we give the rate of primary production proportional to the amount of POM. Let Pr (unit: 1/d) be its proportionality constant (primary production rate per unit of POM per day), for example, Pr = 1 to 5 (1/d) If Pr = 5, then on day 1 of the model calculation, PP (μmol (C)/L /d) = 0.1 (μmol (C)/L ) × Pr (1/d ) = 0.5 (μmol (C)/L /d), but in three days it will exceed 10.6 μmol (C)/L and be in overshoot. In the actual ocean, the peak of the bloom may occur two to four weeks after the phytoplankton increase in early spring.
② Vary the ratio of N to P uptake by primary production. Assume that if nutrients are abundant, they are taken up at an N/P ratio = 10. (We tentatively set the ratio to 10 because it can range from N/P = 8.2 during the log growth phase to an average N/P = 16.) We may give NO3- > 1 μmol/L and PO43- > 0.5 μmol/L as nutrient abundance conditions. As nutrient concentrations at which primary production is severely limited, you might tentatively give NO3- < 0.1 μmol/L and PO43- < 0.05 μmol/L. Once the nutrients reach these concentrations, we can assume that primary production stops. In some cases, once primary production in blooms stops, slow primary production may continue to occur as organic particles stored in surface seawater decompose. (We have seen this happen in the actual ocean as well.)
③ In combination with ① and ②, the primary production rate is lowered to 1/10 of the normal rate in nutrient-poor situations (concentrations at which primary production is severely limited ~ twice its concentration).
The following are considered too high a hurdle to tackle in a report assignment.
④ Vary the rate of sedimentation and removal from the surface layer. Gives the predation rate of zooplankton, the assimilation rate, the excretion rate, the sedimentation and removal rate of fecal grains, etc.
⑤ Consider the depth of the mixed layer. Consider changes in the depth of light transmission. Establish night and day, (this will be a difficult task).
⑥ Add the nutrient component silicon (Si) and set the phytoplankton types to diatoms (which require Si) and dinoflagellates (which do not require Si). Assume that the growth rate of diatoms is greater in nutrient-rich conditions.
⑦ Considering large predators......
Estimation of primary production rate (PP) In the above calculation, PP = 10.6 μmol (c) /L/d was given. The average value of 9.4 μmol (c) /L/d (= 5.5 g C/m3/49d; Table 2 of Maita and Odate, 1988) was reported for the spring bloom period (March-April: 49days) of diatom blooms in Eruption Bay, Hokkaido. PP=10.6 μmol (c)/L/d seems a reasonable value.
For reference, the chlorophyll (Chl.a), particulate organic carbon (POC) (estimated from chlorophyll concentrations), phosphoric acid (PO4), and nitric acid (NO3) concentrations in the surface layer of Eruption Bay from before to after the bloom are summarized below.
chla
(µg/L)POC
(µmol (C)/L)PO4
(µmol/L)NO3
(µmol/L)2019.2.15 0.78 2.3 0.88 9.1 3.4 21 63 0.39 0.28 3.15 11 33 0.36 0.78 4.14 0.19 0.57 0.31 0.05 5.12 0.41 1.23 0.1 0.05 In the table above, the organic carbon concentration (OC (µmol (C)/L ) = 3 x chl.a (µg/L)) was calculated in a rather rough way.(see values of 3-4 readings in the reported results of an iron application experiment conducted in the western subarctic North Pacific).In the 2019 eruption bay, the bloom is likely to end due to nitrate depletion. After April, when the bloom ended, chl.a concentrations increased in May. Can this be explained by regenerative production? If it can be explained by regenerative production, what model parameter values would need to be set? Such an operation is called tuning of model parameters. If it cannot be explained by realistic tuning, we may need to consider other factors (e.g., nutrient supply from external sources).The "marine ecosystem model" used in actual research is the one to figure out these factors.（You can add as many conditions as you want. (You can add as many conditions as you like, but if you get tired, please stop in the middle.)There are studies, which is analyzing models of primary production and secondary production (zooplankton as prey) in the North Pacific subarctic region, including salmon migration locations and growth histories. The effects of global warming are also analyzed. The following are the research results of Dr. Kishi's group, Professor Emeritus of the Faculty of Fisheries, Hokkaido University. Currently, Professor Ueno of the Department of Marine Science and Resources has taken over the group's work. Researchers in the physical sciences are conducting model analysis of marine biology and chemistry.
Below are the research papers of Dr. Kishi's group on marine ecosystem models. -
This study uses a marine ecosystem model (North Pacific subarctic version: NEMURO) to analyze the growth and distribution of Japanese-style salmon. Get the full text (PDF) from the download site.
-
A calculation sheet will be distributed as an example. Feel free to rewrite the calculation method and try out the model calculations.
-