機械的分離操作
โครงสร้างหัวข้อ
-
-
1-1．頻度分布曲線
任意の粒子径範囲にある粒子の質量あるいは体積の頻度
頻度が最大の粒子径が「モード径」
1-2．残留率曲線（R 曲線，フルイ上曲線）
粒子径と同じサイズの目のフルイ上に「残留」する粒子の質量あるいは体積の分率
残留率が 50% となる粒子径が「メディアン径」
1-3．通過率曲線（P 曲線，フルイ下曲線）
粒子径と同じサイズの目のフルイを「通過」する粒子の質量あるいは体積の分率
通過率（P） = 1 – 残留率（R）
1-4．Rosin-Rammler 分布
実際の粉体や穀物粒子の粒子径分布によく合う経験式
R = exp[-(D/De)ⁿ] (1-1)
D は粒子径，De は残留率37%の粒子径，n 値が大きいほど粒子径が揃っている
-
-
-
流体中における粒子の運動方程式（慣性力＝重力－浮力－抵抗力）
(2-1)CD 流体の抵抗係数，D 粒子直径，t 時間，u 粒子沈降速度，ρ 流体密度，ρs 粒子密度
流体に微粒子を落とすと，最初は加速運動をするが，すぐに等速運動（du/dt = 0）になる。これを終末沈降速度（terminal velocity）とよぶ。
ut = ( ρs– ρ)gD²/18μ (2-2)
ut (m/s) 終末沈降速度，μ (Pa·s) 流体の粘度，流体の密度，粒子の密度
粒子の終末沈降速度は，流体と粒子の密度差に比例，粒子径の2 乗に比例
-
-
-
3-1．アンドレゼン・ピペット法
アンドレゼン・ピペット（右図）を用いた粒子径測定操作は，以下のように非常に簡単である。
1）アンドレゼン・ピペットに所定量の液体と粉体を加えてよく撹拌した後に静置
2）上部に取り付けたピペットで所定時間に試料液を採取し固形分の濃度を測定
3）通常は，採取した試料液を乾燥して残った固形分の質量を測定して濃度を決定
試料液中の固形分の質量は，時間の経過とともに減少する。減少した質量は，静置してから試料を採取するまでの間（時間t）に，液面からピペット先端（距離H）を通過できる沈降速度をもつ粒子群の質量に等しい。よって，時間t に採取した試料液の固形分濃度C を初濃度C0 で割った値は，終末沈降速度がH/t より遅い粒子群の割合（通過率）に相当し，Stokes 式（式2-2）によって採取時間を粒子径に変換すると通過率曲線を描くことができる。
-
3-2．沈降天秤法
左下図の沈降管によく撹拌した懸濁液を入れ，トラップに堆積する固体質量の経時変化を測定すると，右下図のようなグラフ（沈降曲線）が得られる。粒径が均一な場合は質量が直線的に増加し，不均一な場合は曲線をとなる。時間tにおける堆積重量をWt，重量が変化しなくなったときの重量をWf とすると，残留率R [-]は，
(3-1)式3-1 をt について微分すると，
(3-2)式3-1 と3-2 から，
(3-3)粒子の密度および流体の密度と粘度がわかれば，Stokes 式により時間を粒径に換算することができる。一方，沈降曲線の接線の切片は残留率R に等しいので，この結果から，残留率曲線を描くことができる。
-
-
4-1．ろ過
基本式（Lewis 式）は，
(4-1)v（m/s） ろ液流束，A（m2） ろ過面積，V（m3） ろ液量，t（s） ろ過時間，μ（kg/m·s） 流体粘度，ΔP（Pa） ろ過圧力, Rm ろ材（ろ紙や膜）抵抗係数，Rc （m-1） ろさい（ケーク，ろ材上に堆積する固体）抵抗係数
ろ材の抵抗係数は，ろ過操作中に目詰まりが起こらなければ一定である。一方，ケーク抵抗はろ材上への固形分の堆積とともに増加，ケークが非圧縮性の場合，
Rc = αCV/A (4-2)
α（m/kg） ケーク比抵抗，C（kg/m3） ろ過原液の固形分濃度
式4-1 と式4-2 から，
(4-3)工業規模では，圧力を制御してろ液の流速を一定に保つ「定速ろ過」と，圧力を一定に保つ「定圧ろ過」が利用される。
-
4-1-1．定速ろ過
定速ろ過ではdV/dt = V/t なので，
(4-4)よって，定速ろ過のΔP vs V プロットは直線となり，傾きからケーク比抵抗α，切片からろ材抵抗係数Rm が得られる。
4-1-2．定圧ろ過
定圧ろ過ではΔP が一定なので，
(4-5)式4-5 はRuth 式とよばれ，定圧ろ過においてはt/V vs V のプロットが直線となり，傾きからケーク比抵抗α，切片からろ材の抵抗係数Rm が得られる。
4-1-3．重力ろ過
実験ではロートとろ紙を使った「重力ろ過」が多い。重力ろ過では，ろ過圧力がろ液量に比例して低下するので，
(4-6)ρ（kg/m3） 流体密度，g （m/s2） 重力加速度，h0 （m） ろ過原液の液深，Av（m2） ろ過器の断面積
式4-6 をt = 0 からt，V = 0 からV で積分すると，
(4-7)式4-7において，α以外は，装置仕様，操作条件，実験結果なので，上式の左辺をy軸，右辺のα以外をx軸にとったプロットは直線となり，傾きからαが得られる。また，ろ過原液が固形分を含まない場合はC = 0なので，
(4-8)よって，水の透過実験の結果に式3-8を適用すると，傾きからRmが得られる。
-
4-2．遠心分離
半径r の円周上を角速度ω（rad）で運動する質量mの物体に働く遠心力Fは，
F = mrω² (4-9)
遠心分離機を回転数Nで運転しているとき，中心からrにある物体が1秒間に移動する距離Lは，
L = 2πrN (4-10)
遠心分離機の仕様書では回転数をr.p.m （revolution per minute）で表記していることが多い。国際単位では秒単位のr.p.sに換算すること。角速度1 radは半径と同長の孤がなす角度なので，
ω = 2πrN/r = 2πN (4-11)
式4-9と4-11より，
F = 4mπ²N²r (4-12)
式4-12の遠心力と万有引力mgの比が遠心効果xである。
x = 4mπ²N²r /mg = 4π²N²r/g (4-13)
通常，遠心力は10 Gや100 Gと表記され，数字が遠心効果xを，Gが重力加速度を表す。ここで，重力加速度を大文字のGで表すのは，質量のgと区別するためである。
4π²N²r = xg ≡ xG (4-14)
遠心場で流体中を沈降する粒子の推進力は遠心力なので，Stokes式の重力加速度を式4-14で置き換えると，
(4-15)遠心力は，回転軸の中心から粒子までの距離rの関数なので，
ut = dr/dt (4-16)
式4-15と4-16から，遠心分離によって粒子が遠沈管の底に沈む時間を求めることができる。
-
-
-
5-1．粒子間に働く静電気的反発力
5-1-1．粒子の表面電荷
液相と接する固相や気相の界面は負に帯電していることが多い。これは，陽イオンの方が水和されやすく，液相で安定化するためである。無機物だけでなく有機物の表面も中性pH以上で負に帯電する。微生物の場合は，表面のカルボキシル基やリン酸基が負電荷，アミノ基やイミダゾル基などが正電荷の要因となる。そのため，アミノ基やイミダゾル基が電荷を失うアルカリ性域で全体が負電荷，カルボキシル基やリン酸基が電荷を失う低pHで全体が正電荷をもち，同じ表面電荷の同種粒子間に「静電気的反発力」が働く。
5-1-2．電気二重層
負に帯電した固体表面には陽イオンが引きつけられる。一方，水中の微粒子はブラウン運動をしているので，粒子表面近傍の正電荷は，表面に近いほど密度が高い拡散分布となる（Gouy-Chapman拡散二重層モデル)。
Φ = Φ0 exp(-κL) (5-1)
Φ 粒子表面から距離Lにおける電位，Φ0 表面電位，κ Debyeパラメータ
距離L = 1/κは「電気二重層の厚さ」とよばれ，液相イオン強度が高くなると，1/κが小さくなる。これを「電気二重層の圧縮」という。
5-1-3．電気二重層によって生じる反発力
同じ電荷とサイズの球形粒子間に働く静電気的反発力VRは，
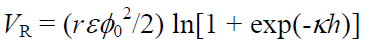(5-2)r 粒子の半径，h 粒子間の距離，ε 液相の誘電率
5-2．粒子間に働く引力（van der Waals力）
物質を構成する分子の間にはvan der Waals引力が働く。van der Waals引力は以下の三つの力からなる。
1） 双極子間引力：分子内の電子分布が非対称な分子が永久双極子となって働く引力
2） 誘起効果：永久双極子をもつ分子に隣接する分子が分極して働く引力
3） London分散力：極性が小さく永久双極子をもたない分子間に働く普遍的な分子間引力。分子間距離の7乗に反比例する近距離引力であるが，コロイドサイズの分子集合体の場合はかなり遠距離に及ぶ
-