Again, let us take the expansion and contraction of volume under constant temperature conditions as an example.
Now consider the entropy change and internal energy change when the volume changes.
Internal energy is defined as "the sum of the kinetic energies of the molecules composing the system".
Internal energy is "proportional to temperature."
(I'll add a little more about internal energy later.)
As shown in the picture below, the gas expands or contracts at a constant temperature. Since the temperature is constant, the internal energy does not change before or after the expansion or contraction. As explained in the previous course, if the volume increases tenfold at a constant temperature, entropy increases by only 19.3 (J/K).
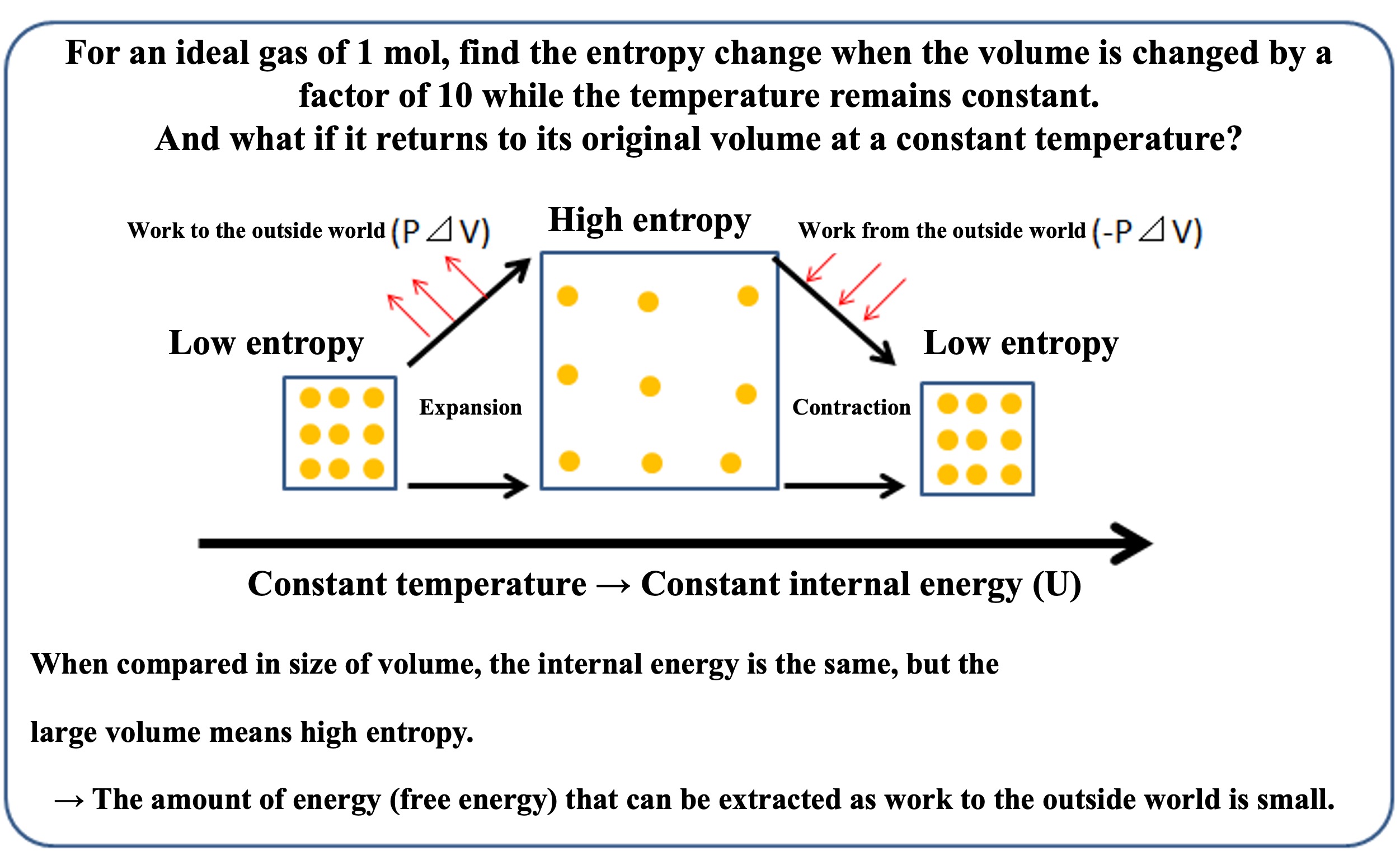
Conversely, if work is applied externally to contract the volume and the temperature is kept constant, entropy is reduced by only 19.3 (J/K) compared to before the contraction, even though the internal energy is maintained the same.
In other words, entropy can be reduced by adding the energy required to adjust the aggregate state. Since the internal energy is only proportional to the temperature T0*, the internal energy of the system does not change before or after expansion or contraction.
High entropy before contraction has a large amount of "bound energy" that cannot be extracted by work to the outside world.
※ The nature of internal energy will be explained in a later course.