セクションアウトライン

    • 　再び、温度一定条件における体積の膨張・収縮を例にだします。


      　今度は、体積が変化したときのエントロピー変化と内部エネルギー変化について考えます。

      内部エネルギーとは、「系を構成する分子の運動エネルギーの総和」と定義され、

      内部エネルギーは「温度に比例する」

      （内部エネルギーについては、あとで少し補足します）


      　下の絵のように、温度一定のまま、気体を膨張させたり、収縮させたりする。温度一定なのだから、膨張や収縮の前後で内部エネルギーは変わりません。先のコースで説明したように、温度一定で体積が10倍に増えれば、エントロピーは19.3 (J/K)だけ増えます。





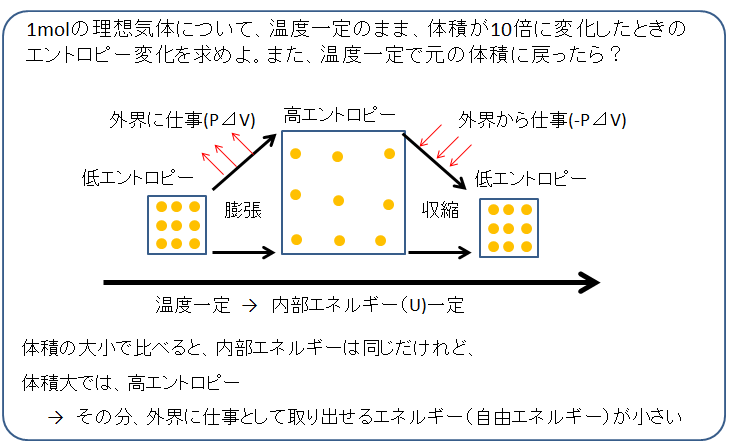
      　逆に、外部から仕事を与え、体積を収縮させて、温度一定に保てば、内部エネルギーは同じなのに、収縮前に比べてエントロピーは19.3 (J/K)だけ減ります。

      　つまり、集合状態を調整するのに要するエネルギーを加えてやれば、エントロピーを減らすことができます。内部エネルギーは温度T0に比例するだけなので※、系がもつ内部エネルギーは膨張・収縮前後で変わりません。

      　収縮前の高エントロピーの方は、外界に仕事して取り出せない“束縛エネルギー”が大きいのです。


        ※ 内部エネルギーの正体については、あとのコースで説明します。