硫黄（S）のプールべ図
Section outline
-
-
E = 0.25 － 0.06648×pH (式1)
式1を、横軸pH、縦軸E(V)にして、下のグラフに示します。なお、図中のSO42-⇔HS-ライン（黒色太線）が、上で求めた境界条件になります。
酸素が豊富な海水(pH8)の酸化還元電位を測定してみると、+0.3～+0.6 (V)くらいです。（純水に酸素だけを十分量溶解させると、その水の酸化還元電位は+0.8 (V)になりますが、自然水中には還元物質（有機物など）も含まれるため、海水では+0.6 (V)より小さくなります）
この図より、酸素を含む海水（E = 0.3～0.6 V）において硫黄(S)は、SO42-として安定に存在することが判断できます。
堆積物中で酸素がゼロになると、酸化還元電位が急に低します。さらに、硝酸などの酸化剤までなくなると、酸化還元電位がSO42-⇔HS-のラインを下回ります。すると、堆積物中では、硫酸(SO42-)を酸化剤として呼吸する“硫酸還元バクテリア”が増殖し、間隙水中のSO42-を硫化水素(H2S)に変えてゆきます。なお、堆積物中では、有機物分解にともない炭酸が発生するので若干酸性化してpH7くらいになります。堆積物中での酸化還元電位とpHの低下の様子を図中の緑の破線矢印で記しました。 -
先ほどは、[SO42-] / [HS-] = 1 の条件式（Eh = 0.25 - 0.06648×pH）
を、プールべ図にプロットしました。違う比率ではどうなるでしょうか・
[SO42-] / [HS-] = 1000 の条件では、Eh = 0.27 - 0.06648×pH になります。電位が+0.02だけシフトしました。図にすると、先ほどとほとんど変わりません。つまり、このプロットの近くで、[SO42-] と [HS-] の比率が急激に変わることを意味します。
-
また、硫化水素イオン(HS-)は、硫化水素(H2S)と解離平衡にあります。
硫化水素と硫化水素イオンの解離平衡の反応式
H2S (aq) = H+ + HS- ；K = 10－7 （Kは、解離平衡定数）
この反応でSの酸化数は－2価で変わらないので、これは酸塩基反応である。したがって、この解離平衡の条件において酸化還元電位は関係ありません。平衡定数とpHの関係は以下の式で表されます。
平衡定数 = ｛生成形の濃度積｝ / ｛原形の濃度積｝ だから、
[HS-][H+] / [H2S]} = 10－7
両辺Logをとって、水素イオン濃度をpHで表します。
Log{ [HS-] / [H2S] } － pH = －7
HS-とH2Sが同じ比率で共存する平衡条件：[HS-] / [H2S] = 1 はpH = 7のときです。
pH7以下では、ほとんどがH2Sとして存在し、pH7以上であればHS-として存在することになります。この情報を加えて、先の図を書きなおしました。
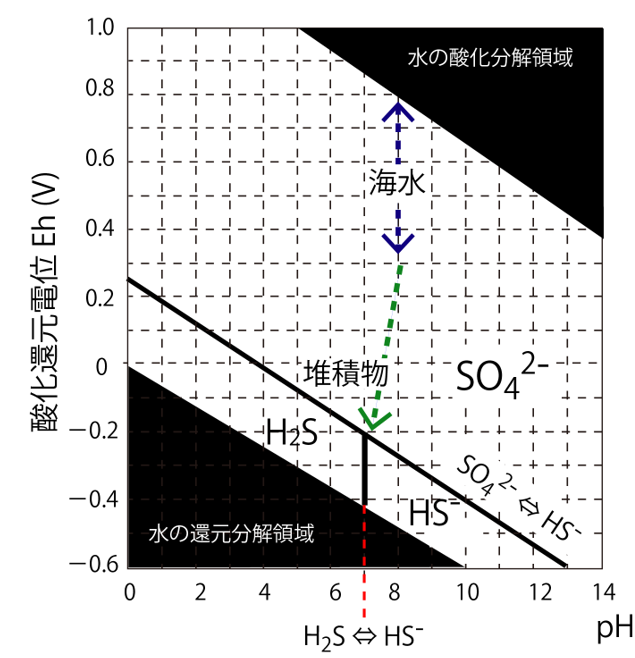
これを、物質の化学形態がpHと酸化還元電位で変わることを表す、“プールベ図”といいます。「水の酸化分解領域」と「水の還元分解領域」では、H2Oが分解してしまう領域のため、水環境では存在しえない領域です。
繰り返しになりますが、プールベ図で記した境界条件は、熱力学定数から計算した結果であり、微生物の作用により、より酸化的な環境（－0.1 (V)くらいから）でも硫酸還元が進むことが確認されています。 -
-